已知一个圆的半径为5cm，则它的内接正六边形的边长为 cm．
【答案】5
【解析】
试题分析：首先根据题意画出图形，六边形ABCDEF是正六边形，易得△OAB是等边三角形，又由圆的半径为5cm，即可求得它的内接六边形的边长=5cm．
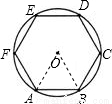
考点：圆内接正六边形
【题型】填空题
【适用】一般
【标题】2016届江苏省滨海县一中九年级上学期期中考试数学试卷（带解析）
【关键字标签】
【结束】
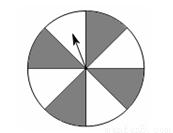
有一个能自由转动的转盘如图，盘面被分成8个大小与形状都相同的扇形，颜色分为黑白两种，将指针的位置固定，让转盘自由转动，当它停止后，指针指向白色扇形的概率是 ．
全能练考卷系列答案
一课一练课时达标系列答案科目：初中数学 来源：2016届江苏省九年级上学期期中考试数学试卷（解析版） 题型：解答题
在平面直角坐标系中，已知抛物线
（a，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（﹣4，3），直角顶点B在第二象限．
（1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；
（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q，判断线段PQ的长度是否为定值？如果是，求出PQ的长；如果不是，说明理由；
（3）在（2）的条件下，若点M在直线AC下方，且为平移前（1）中的抛物线上的点，以M、P、Q三点为顶点的三角形是等腰直角三角形，求出所有符合条件的点M的坐标．
查看答案和解析>>
科目：初中数学 来源：2016届江苏省大丰市九年级上学期期中考试数学试卷（解析版） 题型：填空题
如图，在扇形OAB中，∠AOB=90°，半径OA=2．将扇形OAB沿过点B的直线折叠．点O恰好落在弧AB上点D处，折痕交OA于点C，则整个阴影部分的面积为 ．
查看答案和解析>>
科目：初中数学 来源：2016届江苏省九年级上学期期中考试数学试卷（解析版） 题型：解答题
滨海县为创建“文明卫生城市”，积极投入资金进行城市道路建设与园林绿化两项工程，已知2012年投资1000万元，预计2014年投资1210万元．若这两年内平均每年投资增长的百分率相同．
（1）求平均每年投资增长的百分率；
（2）按此增长率，计算2015年投资额能否达到1360万元？
【答案】（1）10%；（2）不能达到
【解析】
试题分析：（1）根据增长率问题的变换可由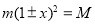
，求得增长的百分率；
（2）根据增长率求出2015年的投资额，然后比较即可．
试题解析：【解析】
（1）设平均每年投资增长的百分率是x．
由题意得1000（1+x）2=1210
解得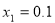
，
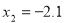（不合题意舍去）．
答：平均每年投资增长的百分率为10%．
（2）∵
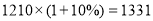＜1360
∴不能达到
考点：一元二次方程的增长率问题
【题型】解答题
【适用】一般
【标题】2016届江苏省滨海县一中九年级上学期期中考试数学试卷（带解析）
【关键字标签】
【结束】
如图，AC是⊙O的直径，点B、D在⊙O上，点E在⊙O外，∠EAB＝∠D＝30°．
（1）∠C的度数为 °；
（2）判断直线AE与⊙O的位置关系，并说明理由；
（3）当AB＝2时，求图中阴影部分的面积（结果保留根号和π）．
查看答案和解析>>
科目：初中数学 来源：2016届江苏省九年级上学期期中考试数学试卷（解析版） 题型：解答题
如图，⊙O的半径为3，P是CB延长线上一点，PO=5，PA切⊙O于A点，则PA= ．
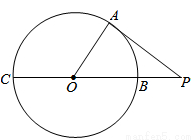
【答案】4
【解析】
试题分析：根据PA是圆的切线，可知OA⊥PA，然后根据勾股定理可得PA=4．
考点：切线的性质，勾股定理
【题型】填空题
【适用】一般
【标题】2016届江苏省滨海县一中九年级上学期期中考试数学试卷（带解析）
【关键字标签】
【结束】
用适当的方法解下列方程：
（1）
；
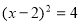（2）
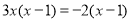
查看答案和解析>>
科目：初中数学 来源：2016届湖北省宜昌市点军区九年级上学期期中考试数学试卷（解析版） 题型：选择题
已知x2+y2-4x+6y+13=0，则代数式x+y的值为（ ）．
A．-1 B．1 C．5 D．36
查看答案和解析>>
科目：初中数学 来源：2016届广东省深圳市九年级月考一数学试卷（解析版） 题型：填空题
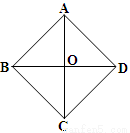
如图所示，在四边形ABCD中，AB＝BC＝CD＝AD，对角线AC与BD相交于点O．若不增加任何字
母与辅助线，要使得四边形ABCD是正方形，则还需增加的一个条件是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的根为 ．
、
是一元二次方程
的两个根，则
等于（ ）
B．
C．1 D．4