
分析 根据三角形的周长公式可得:底边长=周长-2×腰长;再根据三角形三边关系定理:三角形任意两边之和大于第三边可得$\left\{\begin{array}{l}{2x>y}\\{x+y>x}\end{array}\right.$,再把y=12-2x代入可得$\left\{\begin{array}{l}{2x>12-2x}\\{12-2x>0}\end{array}\right.$,再解不等式组即可.
解答 解:依题意有:y=12-2x,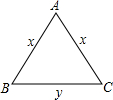
故y与x的函数关系式为:y=12-2x;
∵$\left\{\begin{array}{l}{2x>y}\\{x+y>x}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2x>12-2x}\\{12-2x>0}\end{array}\right.$,
解得:3<x<6.
故自变量x的取值范围为3<x<6.
故答案为:y=12-2x;3<x<6.
点评 此题主要考查了列函数关系式,此题的难点是求自变量x的取值范围,关键是掌握三角形任意两边之和大于第三边.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
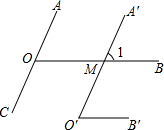 如图所示,OA∥O′A′,OB∥O′B′.
如图所示,OA∥O′A′,OB∥O′B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com