
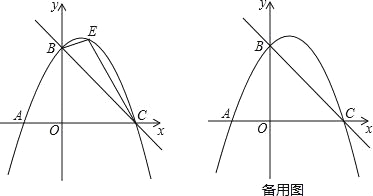
【题目】如图,直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)(2,3),3;(3)(﹣3,﹣
x+3;(2)(2,3),3;(3)(﹣3,﹣![]() )、(5,﹣
)、(5,﹣![]() )、(﹣1,
)、(﹣1,![]() ).
).
【解析】
试题分析:(1)∵直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0),∵抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0),∵抛物线y=ax2+![]() x+c经过B、C两点,∴
x+c经过B、C两点,∴ ,解得
,解得 ,∴y=﹣
,∴y=﹣![]() x2+
x2+![]() x+3.
x+3.
(2)如图1,过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F,
 ,
,
∵点E是直线BC上方抛物线上的一动点,∴设点E的坐标是(x,﹣![]() x2+
x2+![]() x+3),则点M的坐标是(x,﹣
x+3),则点M的坐标是(x,﹣![]() x+3),∴EM=﹣
x+3),∴EM=﹣![]() x2+
x2+![]() x+3﹣(﹣
x+3﹣(﹣![]() x+3)=﹣
x+3)=﹣![]() x2+
x2+![]() x,∴S△BEC=S△BEM+S△MEC=
x,∴S△BEC=S△BEM+S△MEC=![]() =
=![]() ×(﹣
×(﹣![]() x2+
x2+![]() x)×4=﹣
x)×4=﹣![]() x2+3x=﹣
x2+3x=﹣![]() (x﹣2)2+3,∴当x=2时,即点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3.
(x﹣2)2+3,∴当x=2时,即点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3.
(3)在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.
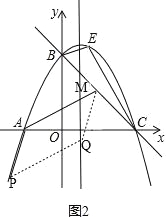
①如图2,
 ,
,
由(2),可得点M的横坐标是2,∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ),又∵点A的坐标是(﹣2,0),∴AM=
),又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∴AM所在的直线的斜率是:
,∴AM所在的直线的斜率是: ;∵y=﹣
;∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则 ,解得
,解得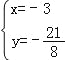 或
或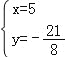 ,∵x<0,∴点P的坐标是(﹣3,﹣
,∵x<0,∴点P的坐标是(﹣3,﹣![]() ).
).
②如图3,
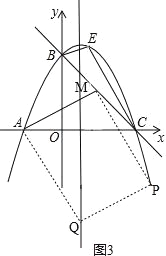 ,
,
由(2),可得点M的横坐标是2,∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ),又∵点A的坐标是(﹣2,0),∴AM=
),又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∴AM所在的直线的斜率是:
,∴AM所在的直线的斜率是: ;∵y=﹣
;∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则 ,解得
,解得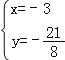 或
或 ,∵x>0,∴点P的坐标是(5,﹣
,∵x>0,∴点P的坐标是(5,﹣![]() ).
).
③如图4,
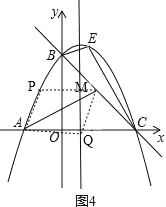 ,
,
由(2),可得点M的横坐标是2,∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ),又∵点A的坐标是(﹣2,0),∴AM=
),又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∵y=﹣
,∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则 解得
解得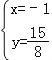 ,∴点P的坐标是(﹣1,
,∴点P的坐标是(﹣1,![]() ).综上,可得在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,点P的坐标是(﹣3,﹣
).综上,可得在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,点P的坐标是(﹣3,﹣![]() )、(5,﹣
)、(5,﹣![]() )、(﹣1,
)、(﹣1,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]()
![]() ﹣
﹣![]() x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
(1)求点A和点B的坐标;
(2)求证:四边形DECF是矩形;
(3)连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
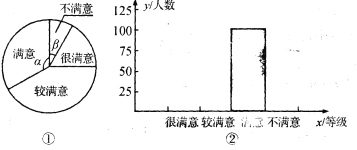
【题目】某学校认真开展学习和实践科学发展观活动,在阶段总结中提出对本单位今后的整改措施,并在征求教职工对整改方案的满意程度时进行民主测评,测评等级为:很满意、较满意、满意、不满意四个等级.
(1)若测评后结果如扇形图(图①),且测试等级为很满意、较满意、满意、不满意的人数之比为3:6:5:1,则图中a= 度,β= 度.
(2)若测试后部分统计结果如直方图(图②),请将直方图补画完整,并求出该单位职工总人数为 人.
(3)按上级要求,满意度必须不少于95%方案才能通过,否则,必须对方案进行完善.若要使该方案完善后能获得通过,至少还需增加 人对该方案的测评等级达满意(含满意)以上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善居民住房条件,某市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为20平方米提高到28.8平方米,若每年的年增长率相同,则年增长率为
A.20% B.10% C.2% D.0.2%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是 ( )
A. 两角对应相等的两个三角形相似 B. 两边对应成比例的两个三角形相似
C. 两边对应成比例且夹角相等的两个三角形相似 D. 三边对应成比例的两个三角形相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.必然事件的概率为1
B.数据6、4、2、2、1的平均数是3
C.数据5、2、-3、0、3的中位数是2
D.某种游戏活动的中奖率为20%,那么参加这种活动100次必有20次中奖
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com