
【题目】如图,已知抛物线y=![]()
![]() ﹣
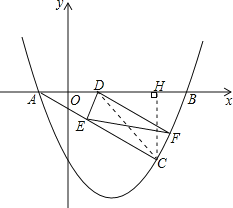
﹣![]() x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
(1)求点A和点B的坐标;
(2)求证:四边形DECF是矩形;
(3)连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.

【答案】(1)(﹣1,0),(4,0);(2)证明过程见解析;(3)2.
【解析】
试题分析:(1)、根据抛物线的解析式来求点A、B的坐标即可;(2)、欲证明四边形DECF是矩形,只需证得四边形DECF是平行四边形且有一内角为直角即可;(3)、连接CD,根据矩形DECF的对角线相等得到:EF=CD.当CD⊥AB时,CD的值最小,即EF的值最小.
试题解析:(1)、当y=0时,![]()
![]() ﹣
﹣![]() x﹣2=0, 解方程,得 x1=﹣1,x2=4. ∵点A在点B的左侧,
x﹣2=0, 解方程,得 x1=﹣1,x2=4. ∵点A在点B的左侧,
∴点A、B的坐标分别是(﹣1,0),(4,0);
(2)、把C(m,1﹣m)代入y=![]()
![]() ﹣
﹣![]() x﹣2得:
x﹣2得:![]() -2=1-m 解方程,得m=3或m=﹣2.
-2=1-m 解方程,得m=3或m=﹣2.
∵点C位于第四象限, ∴m>0,1﹣m<0,即m>1, ∴m=﹣2舍去, ∴m=3,
∴点C的坐标为(3,﹣2). 过点C作CH⊥AB于H,则∠AHC=∠BHC=90°.
由A(﹣1,0),B(4,0),C(3,﹣2)得到:AH=4,CH=2,BH=1,AB=5, ∴![]() =2.
=2.
又∵∠AHC=∠CHB=90°,∴△AHC∽△CHB, ∴∠ACH=∠CBH. ∵∠CBH+∠BCH=90°,
∴∠ACH+∠BCH=90°, ∴∠ACB=90°, ∵DE∥BC,DF∥AC, ∴四边形DECF是平行四边形,
∴平行四边形DECF是矩形;
(3)、存在.理由如下: 连接CD. ∵平行四边形DECF是矩形, ∴EF=CD.
当CD⊥AB时,CD的值最小. ∵C(3,2), ∴DC的最小值是2, ∴EF的最小值是2.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是
A、三角形 B、线段 C、矩形 D、正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产一种袋装食品的标准重量是500克,质检员把每袋超出的部分记作正数,不足的部分记作负数,质检员随机测得一袋食品质量为501克,则记作( )
A. ﹣1 B. 1 C. 0 D. 501
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对“0”的说法正确的个数是( )
①0是正数和负数的分界点;②0只表示“什么也没有”;③0可以表示特定的意义,如0℃;④0是正数;⑤0是自然数.
A. 3个 B. 4个 C. 5个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 一个正数的前面加上负号就是负数 B. 不是正数的数一定是负数
C. 0既不是正数,也不是负数 D. 正负数可以用来表示具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
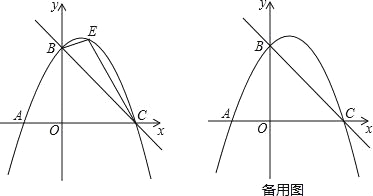
【题目】如图,直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com