
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上一个动点,过点
边上一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
(1)探究![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)当点![]() 运动到
运动到![]() 上的什么位置时,四边形
上的什么位置时,四边形![]() 是矩形,请说明理由;
是矩形,请说明理由;
(3)在(2)的基础上,![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?为什么?
是正方形?为什么?
【答案】(1)OE=OF,理由见解析;(2)当点O运动到AC的中点时,四边形AECF是矩形.理由见解析;(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由见解析;
【解析】
(1)由平行线的性质和角平分线定义得出∠OEC=∠OCE,∠OFC=∠OCF,根据“等角对等边”得出OE=OC,OF=OC,即可得出结论;
(2)由(1)得出的OE=OC=OF,点O运动到AC的中点时,则由OE=OC=OF=OA,证出四边形AECF是平行四边形,再证出∠ECF=90°即可;
(3)由已知和(2)得到的结论,点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,则推出四边形AECF是矩形且对角线垂直,得出四边形AECF是正方形.
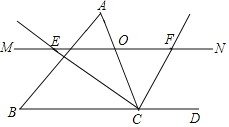
(1)OE=OF,理由如下:
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠DCF,
∵CE平分∠BCA,CF平分∠ACD,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴OE=OC,OF=OC,
∴OE=OF;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.
∵当点O运动到AC的中点时,AO=CO,
又EO=FO,
∴四边形AECF为平行四边形,
又CE为∠ACB的平分线,CF为∠ACD的平分线,
∴∠BCE=∠ACE,∠ACF=∠DCF,
∴∠BCE+∠ACE+∠ACF+∠DCF=2(∠ACE+∠ACF)=180°,
即∠ECF=90°,
∴四边形AECF是矩形;
(3)解:当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由如下:
∵由(2)知,当点O运动到AC的中点时,四边形AECF是矩形,
∵MN∥BC,
当∠ACB=90°,则∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.


科目:初中数学 来源: 题型:
【题目】若关于x、y的二元一次方程组![]() 的解都为正数.
的解都为正数.
(1)求![]() 的取值范围;
的取值范围;
(2)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学校图书馆上个月借阅情况,管理老师从学生对艺术、经济、科普及生活四类图书借阅情况进行了统计,并绘制了下列不完整的统计图,请根据图中信息解答下列问题:
(1)上个月借阅图书的学生有多少人?扇形统计图中“艺术”部分的圆心角度数是多少?
(2)把条形统计图补充完整;
(3)从借阅情况分析,如果要添置这四类图书300册,请你估算“科普”类图书应添置多少册合适?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,由以上信息能求出CB的长度吗?请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是 cm.
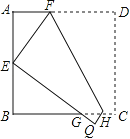
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎疫情肆虐,红星社区为了提高社区居民的身体素质,鼓励居民在家锻炼,特采购了一批跳绳免费发放,已知2根幸福牌跳绳和1根平安牌跳绳共需31元,2根平安牌跳绳和3根幸福牌跳绳共需54元.
(1)求幸福牌跳绳和平安牌跳绳的单价;
(2)已知该社区需要采购两种品牌的跳绳共60根,且平安牌跳绳的数量不少于幸福牌跳绳数量的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com