
【题目】如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).
(1)求抛物线的解析式;
(2)点P是抛物线上的一个动点(不与点A、点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.
①当PE=2ED时,求P点坐标;
②是否存在点P使△BEC为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵点B(4,m)在直线y=x+1上,
∴m=4+1=5,
∴B(4,5),
把A、B、C三点坐标代入抛物线解析式可得  ,解得
,解得  ,
,
∴抛物线解析式为y=﹣x2+4x+5
(2)
解:①设P(x,﹣x2+4x+5),则E(x,x+1),D(x,0),
则PE=|﹣x2+4x+5﹣(x+1)|=|﹣x2+3x+4|,DE=|x+1|,
∵PE=2ED,
∴|﹣x2+3x+4|=2|x+1|,
当﹣x2+3x+4=2(x+1)时,解得x=﹣1或x=2,但当x=﹣1时,P与A重合不合题意,舍去,
∴P(2,9);
当﹣x2+3x+4=﹣2(x+1)时,解得x=﹣1或x=6,但当x=﹣1时,P与A重合不合题意,舍去,
∴P(6,﹣7);
综上可知P点坐标为(2,9)或(6,﹣7);
②设P(x,﹣x2+4x+5),则E(x,x+1),且B(4,5),C(5,0),
∴BE= ![]() =
= ![]() |x﹣4|,CE=
|x﹣4|,CE= ![]() =
= ![]() ,BC=
,BC= ![]() =
= ![]() ,
,
当△BEC为等腰三角形时,则有BE=CE、BE=BC或CE=BC三种情况,
当BE=CE时,则 ![]() |x﹣4|=
|x﹣4|= ![]() ,解得x=
,解得x= ![]() ,此时P点坐标为(
,此时P点坐标为( ![]() ,
, ![]() );
);
当BE=BC时,则 ![]() |x﹣4|=
|x﹣4|= ![]() ,解得x=4+
,解得x=4+ ![]() 或x=4﹣
或x=4﹣ ![]() ,此时P点坐标为(4+
,此时P点坐标为(4+ ![]() ,﹣4
,﹣4 ![]() ﹣8)或(4﹣
﹣8)或(4﹣ ![]() ,4
,4 ![]() ﹣8);
﹣8);
当CE=BC时,则 ![]() =
= ![]() ,解得x=0或x=4,当x=4时E点与B点重合,不合题意,舍去,此时P点坐标为(0,5);
,解得x=0或x=4,当x=4时E点与B点重合,不合题意,舍去,此时P点坐标为(0,5);
综上可知存在满足条件的点P,其坐标为( ![]() ,
, ![]() )或(4+
)或(4+ ![]() ,﹣4
,﹣4 ![]() ﹣8)或(4﹣
﹣8)或(4﹣ ![]() ,4
,4 ![]() ﹣8)或(0,5)
﹣8)或(0,5)
【解析】(1)由直线解析式可求得B点坐标,由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)①可设出P点坐标,则可表示出E、D的坐标,从而可表示出PE和ED的长,由条件可知到关于P点坐标的方程,则可求得P点坐标;②由E、B、C三点坐标可表示出BE、CE和BC的长,由等腰三角形的性质可得到关于E点坐标的方程,可求得E点坐标,则可求得P点坐标.


科目:初中数学 来源: 题型:
【题目】在△ABC纸片中,∠ACB=90°,AC=6,BC=8,沿过其中一个顶点的直线把△ABC剪开,若剪得的两个三角形中仅有一个是等腰三角形,那么这个等腰三角形的面积不可能是( )
A.14.4
B.19.2
C.18.75
D.17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在直线AB上方,且∠APB=90°,PC⊥AB于C,若线段AB=6,AC=x,S△PAB=y,则y与x的函数关系图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
(1)求出下列成绩统计分析表中a,b的值:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.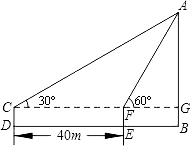
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com