
 如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.
如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.分析 (1)由SSS即可证出结论;
(2)①要四边形OCAF是菱形,需OC=CA=AF=OF,即△AOC为等腰三角形,∠2=60°,那么∠1=30°;②由等腰直角三角形的性质即可得到结论.
解答 (1)证明:∵AB是直径,
∴∠ACB=90°,
∴OC=OB,
∵OD⊥BC于点D,
∴CD=BD,
在△CDO和△BDO中,$\left\{\begin{array}{l}{OC=OB}\\{CD=BD}\\{OD=OD}\end{array}\right.$,
∴△CDO≌△BDO(SSS);
(2)解:当∠1=30°时,四边形OCAF是菱形.
理由如下:
∵∠1=30°,AB是直径,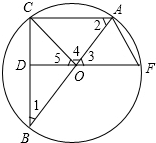
∴∠BCA=90°,
∴∠2=60°,而OC=OA,
∴△OAC是等边三角形,
∴OA=OC=CA,
又∵D,O分别是BC,BA的中点,
∴DO∥CA,
∴∠2=∠3=60°而OC=OA=AF.
∴△OAF是等边三角形,
∴AF=OA=OF,
∴OC=CA=AF=OF,
∴四边形OCAF是菱形;
②当∠1=45°时,AB=2$\sqrt{2}$OD,
∵∠1=45°,
∵OD⊥BC于点D,
∴△BOD是等腰直角三角形,
∴OB=$\sqrt{2}$OD,
∴AB=2OB=2$\sqrt{2}$OD.
点评 本题考查了全等三角形的判定、等边三角形的判定与性质、菱形的判定、圆周角定理、三角形中位线定理;熟练掌握全等三角形的判定和菱形的判定,证明三角形是等边三角形是解决问题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 【阅读理解】我们知道,当a>0且b>0时,($\sqrt{a}$-$\sqrt{b}$)2≥0,所以a-2$\sqrt{ab}$+≥0,从而a+b≥2$\sqrt{ab}$(当a=b时取等号),
【阅读理解】我们知道,当a>0且b>0时,($\sqrt{a}$-$\sqrt{b}$)2≥0,所以a-2$\sqrt{ab}$+≥0,从而a+b≥2$\sqrt{ab}$(当a=b时取等号),查看答案和解析>>
科目:初中数学 来源: 题型:选择题
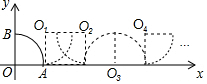 如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )
如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )| A. | (16+4π,0) | B. | (14+4π,2) | C. | (14+3π,2) | D. | (12+3π,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
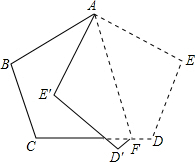 将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在E′,D′点.已知∠AFC=76°,则∠CFD′等于( )
将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在E′,D′点.已知∠AFC=76°,则∠CFD′等于( )| A. | 15° | B. | 25° | C. | 28° | D. | 31° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
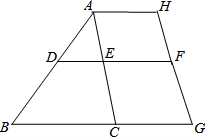 如图:已知∠DAE=55°,∠ADE=60°,∠ACB=65°,∠H与∠G互补,试说明AH∥DF的理由.
如图:已知∠DAE=55°,∠ADE=60°,∠ACB=65°,∠H与∠G互补,试说明AH∥DF的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com