解:(1)∵在矩形ABCD中,BC=6,AB=8.
∴AC=

=10,
,∵BC∥AE,
∴△PBC∽△PEA,
∴

=

=
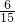
=

,
∴
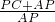
=

,
∴AP=

×10=
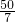
;
(2)∵

≠

,
∴△BAP与△CAB不相似,
∴AP与BE不垂直,
∴BE与⊙A的位置关系为相交;
(3)若以A为圆心,r
1为半径作⊙A,使点D在⊙A内,点B在⊙A外,则r
1的取值范围为0≤r
1<6;
∵r
1+r
2=10,
∴r
1=10-r
2,
∴0≤10-r
2<6,
∴4<r
2≤10.
故答案为0≤r
1<6;4<r
2≤10.
分析:(1)先利用勾股定理计算出AC=10,再证明△PBC∽△PEA,然后利用相似比和比例性质计算AP;
(2)利用

≠

,可判断△BAP与△CAB不相似,则AP与BE不垂直,然后根据直线与圆的位置关系进行判断;
(3)根据点与圆的位置关系得到0≤r
1<6,再利用两圆相切的性质得到r
1=10-r
2,则0≤10-r
2<6,然后解不等式组.
点评:本题考查了圆与圆的位置关系:若两圆的圆心距、半径分别为d、R、r,则①两圆外离?d>R+r;②两圆外切?d=R+r;③两圆相交?R-r<d<R+r(R≥r);④两圆内切?d=R-r(R>r);⑤两圆内含?d<R-r(R>r).也考查了点与圆、直线与圆的位置关系.

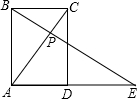 已知:如图,在矩形ABCD中,BC=6,AB=8.延长AD到点E,使AE=15,连接BE交AC于点P.
已知:如图,在矩形ABCD中,BC=6,AB=8.延长AD到点E,使AE=15,连接BE交AC于点P. =10,
=10, =
= =
=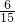 =
= ,
,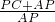 =
= ,
, ×10=
×10=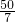 ;
; ≠
≠ ,
, ≠
≠ ,可判断△BAP与△CAB不相似,则AP与BE不垂直,然后根据直线与圆的位置关系进行判断;
,可判断△BAP与△CAB不相似,则AP与BE不垂直,然后根据直线与圆的位置关系进行判断;

 阅读快车系列答案
阅读快车系列答案 已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )
已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( ) 已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.