
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则正方形MNPQ与正方形AEFG的面积之比等于。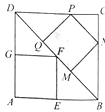
【答案】![]()
【解析】解:在正方形ABCD中
∵![]() ABD=
ABD=![]() CBD=45
CBD=45![]() ,
,
∵四边形MNPQ和AEFG均为正方形,
∴![]() BEF=
BEF=![]() AEF=90
AEF=90![]() ,
,![]() BMN=
BMN=![]() QMN=90
QMN=90![]() ,
,
∴![]() BEF与
BEF与![]() BMN是等腰直角三角形,
BMN是等腰直角三角形,
∴FE=BE=AE=![]() AB,BM=MN=QM,
AB,BM=MN=QM,
同理DQ=MQ,
∴MN=![]() BD=
BD=![]() AB,
AB,
∴正方形MNPQ与正方形AEFG的面积之比=![]() =
=![]() ,
,
故答案为:![]() .
.
根据正方形的对角线性质得到![]() ABD=
ABD=![]() CBD=45
CBD=45![]() ,四边形MNPQ和AEFG均为正方形,推出
,四边形MNPQ和AEFG均为正方形,推出![]() BEF与
BEF与![]() BMN是等腰直角三角形,于是得到FE=BE=AE=
BMN是等腰直角三角形,于是得到FE=BE=AE=![]() AB,BM=MN=QM,同理DQ=MQ,即可得到答案. 此题考查了正方形的性质,等腰直角三角形的性质,正方形面积的计算,熟练掌握等腰直角三角形的性质是解题的关键.
AB,BM=MN=QM,同理DQ=MQ,即可得到答案. 此题考查了正方形的性质,等腰直角三角形的性质,正方形面积的计算,熟练掌握等腰直角三角形的性质是解题的关键.


科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4cm,直线l与⊙O相交于A、B两点,AB=4 ![]() cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 .
cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(2,3),B(1,1),D(4,3),则点P的坐标为( , ). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F分别是ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( ) 
A.6
B.12
C.18
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, ![]() =
= ![]() ,AB=2,连接AC.
,AB=2,连接AC. 
(1)求证:∠CAB=45°;
(2)若直线l为⊙O的切线,C是切点,在直线l上取一点D,使BD=AB,BD所在的直线与AC所在的直线相交于点E,连接AD. (Ⅰ)试探究AE与AD之间的是数量关系,并证明你的结论;
(Ⅱ)是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC= ![]() ,以AB为直径的⊙O分别交BC、AC于点D、E.
,以AB为直径的⊙O分别交BC、AC于点D、E.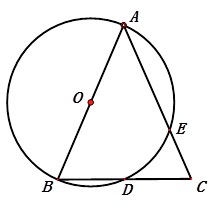
(1)求AE;
(2)过D作DF⊥AC于F,请画出图形,说明DF是否是⊙O的切线,并写出理由;
(3)延长FD,交AB的延长线于G,请画出图形,并求BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个布袋里装有红色、黄色、黑色三个球,它们除颜色外其余都相同,从中任意摸出1个球,记下颜色后放回,搅匀,再摸出1个球.
(1)请用树状图或列表法列举出两次摸球可能出现的各种结果;
(2)摸到的两个球颜色相同的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与A,C重合),DE与AB相交于点F,则图中有( )对相似三角形. 
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com