
【题目】如图,△ABC中,AB=AC=10,BC= ![]() ,以AB为直径的⊙O分别交BC、AC于点D、E.
,以AB为直径的⊙O分别交BC、AC于点D、E.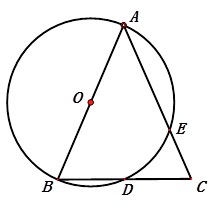
(1)求AE;
(2)过D作DF⊥AC于F,请画出图形,说明DF是否是⊙O的切线,并写出理由;
(3)延长FD,交AB的延长线于G,请画出图形,并求BG.
【答案】
(1)
解:方法一:连结AD、DE
易证BD=CD= ![]() ,
,
△DCE∽△ABC(或△DCA∽△ECB)
∴CE:CB=CB:CA
∴CE=4,AE=6
方法二:BE⊥AC
∴ ![]()
∴ ![]()
∴AE=6
方法三: 易证A D= ![]()
∵BC×AD=AC×BE,
∴BE=8
∴AE=6
(2)
解:DF是⊙O的切线,理由如下:
方法一:BD=CD,OB=OA,
∴OD∥AC
∴DF⊥AC
∴DF是⊙O的切线
方法二:∠ODB=∠B=∠C,
∴OD∥AC
∴DF⊥AC
∴DF是⊙O的切线
(3)
解:方法一: DE=BD= ![]()
∠GBD=∠DEA,∠ GDB=∠FDC=∠DAE
∴ △GBD∽△DEA
∴GB:DE=BD:AE BG= ![]()
方法二:BE∥GF,
∴ △ABE∽△AGF
∴AB:BG=AE:EF
BG= ![]()
【解析】此题考查圆的切线的判定及性质、相似三角形的判定及性质,准确作出辅助线,分析题中图形之间的关系,此题方法较多,理解、分析透彻图形之间、线段之间的关系是解题关键.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2). 
(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD. 
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6.求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队均参与某筑路工程,先由甲队筑路60公里,再由乙队完成剩下的筑路工程,已知乙队筑路总公里数是甲队筑路总公里数的 ![]() 倍,甲队比乙队多筑路20天.
倍,甲队比乙队多筑路20天.
(1)求乙队筑路的总公里数;
(2)若甲、乙两队平均每天筑路公里数之比为5:8,求乙队平均每天筑路多少公里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则正方形MNPQ与正方形AEFG的面积之比等于。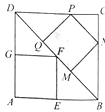
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A,D为圆心,大于 ![]() AD的长为半径在AD两侧作弧,交于M,N两点;第二步,连结MN,分别交AB,AC于点E,F;第三步,连结DE,DF.若BD=6,AF=5,CD=3,则BE的长是( )
AD的长为半径在AD两侧作弧,交于M,N两点;第二步,连结MN,分别交AB,AC于点E,F;第三步,连结DE,DF.若BD=6,AF=5,CD=3,则BE的长是( ) 
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面上有3个点的坐标:A(0,﹣3),B(3,0),C(﹣1,﹣4).
(1)在A,B,C三个点中任取一个点,这个点既在直线y1=x﹣3上又在抛物线上y2=x2﹣2x﹣3上的概率是多少?
(2)从A,B,C三个点中任取两个点,求两点都落在抛物线y2=x2﹣2x﹣3上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com