
分析 (1)利用y轴上点的坐标性质表示出C点坐标,再利用O,C两点间的距离为3求出即可;
(2)分别利用①若C(0,3),即c=3,以及②若C(0,-3),即c=-3,得出A,B点坐标,进而求出函数解析式,进而得出答案;
(3)利用①若c=3,则y1=-x2-2x+3=-(x+1)2+4,y2=-3x+3,得出y1向左平移n个单位后,则解析式为:y3=-(x+1+n)2+4,进而求出平移后的直线与P有公共点时得出n的取值范围,②若c=-3,则y1=x2-2x-3=(x-1)2-4,y2=-3x-3,y1向左平移n个单位后,则解析式为:y3=(x-1+n)2-4,进而求出平移后的直线与P有公共点时得出n的取值范围,进而利用配方法求出函数最值.
解答 解:(1)令x=0,则y=c,
故C(0,c),
∵OC的距离为3,
∴|c|=3,即c=±3,
∴C(0,3)或(0,-3);
(2)∵x1x2<0,
∴x1,x2异号,
①若C(0,3),即c=3,
把C(0,3)代入y2=-3x+t,则0+t=3,即t=3,
∴y2=-3x+3,
把A(x1,0)代入y2=-3x+3,则-3x1+3=0,
即x1=1,
∴A(1,0),
∵x1,x2异号,x1=1>0,∴x2<0,
∵|x1|+|x2|=4,
∴1-x2=4,
解得:x2=-3,则B(-3,0),
代入y1=ax2+bx+3得,$\left\{\begin{array}{l}{a+b+3=0}\\{9a-3b+3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$,
∴y1=-x2-2x+3=-(x+1)2+4,
则当x≤-1时,y随x增大而增大.
②若C(0,-3),即c=-3,
把C(0,-3)代入y2=-3x+t,则0+t=-3,即t=-3,
∴y2=-3x-3,
把A(x1,0),代入y2=-3x-3,
则-3x1-3=0,
即x1=-1,
∴A(-1,0),
∵x1,x2异号,x1=-1<0,∴x2>0
∵|x1|+|x2|=4,
∴1+x2=4,
解得:x2=3,则B(3,0),
代入y1=ax2+bx-3得,$\left\{\begin{array}{l}{a-b-3=0}\\{9a+3b-3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴y1=x2-2x-3=(x-1)2-4,
则当x≥1时,y随x增大而增大,
综上所述,若c=3,当y随x增大而增大时,x≤-1;
若c=-3,当y随x增大而增大时,x≥1;
(3)①若c=3,则y1=-x2-2x+3=-(x+1)2+4,y2=-3x+3,
y1向左平移n个单位后,则解析式为:y3=-(x+1+n)2+4,
则当x≤-1-n时,y随x增大而增大,
y2向下平移n个单位后,则解析式为:y4=-3x+3-n,
要使平移后直线与P有公共点,则当x=-1-n,y3≥y4,
即-(-1-n+1+n)2+4≥-3(-1-n)+3-n,
解得:n≤-1,
∵n>0,∴n≤-1不符合条件,应舍去;
②若c=-3,则y1=x2-2x-3=(x-1)2-4,y2=-3x-3,
y1向左平移n个单位后,则解析式为:y3=(x-1+n)2-4,
则当x≥1-n时,y随x增大而增大,
y2向下平移n个单位后,则解析式为:y4=-3x-3-n,
要使平移后直线与P有公共点,则当x=1-n,y3≤y4,
即(1-n-1+n)2-4≤-3(1-n)-3-n,
解得:n≥1,
综上所述:n≥1,
2n2-5n=2(n-$\frac{5}{4}$)2-$\frac{25}{8}$,
∴当n=$\frac{5}{4}$时,2n2-5n的最小值为:-$\frac{25}{8}$.
点评 此题主要考查了二次函数综合以及二次函数的平移以及二次函数增减性等知识,利用分类讨论得出n的取值范围是解题关键.


科目:初中数学 来源: 题型:选择题
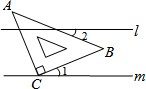 如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )
如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a2)3=6a6 | B. | -a2b2•3ab3=-3a2b5 | ||
| C. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 | D. | $\frac{{a}^{2}-1}{a}$•$\frac{1}{a+1}$=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
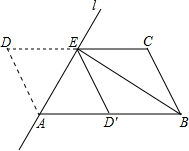 如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.
如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com