
【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.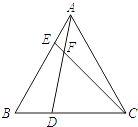
(1)求证:AD=CE;
(2)求∠DFC的度数.
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE
(2)解:
∵(1)△AEC≌△BDA,
∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°
【解析】(1)由等边三角形性质易得∠BAC=∠B=60°,AB=AC;题干给了AE=BD,所以得到△AEC≌△BDA.AD=CE;
(2)由外角关系结合(1)中得到的△AEC≌△BDA易得∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°
【考点精析】根据题目的已知条件,利用等边三角形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】下列各式由左边到右边的变形中,属于分解因式的是( )
A.a(x+y)=ax+ay
B.x2﹣4x+4=x(x﹣4)+4
C.10x2﹣5x=5x(2x﹣1)
D.x2﹣16+6x=(x+4)(x﹣4)+6x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
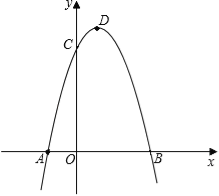
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
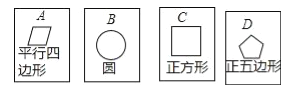
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市辖区内长江流域水质情况的调查
B.对乘坐飞机的旅客是否携带违禁物品的调查
C.对一个社区每天丢弃塑料袋数量的调查
D.对重庆电视台“天天630”栏目收视率的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列关于自然数的等式:
(i)32﹣4×12=5 ①
(ii)52﹣4×22=9 ②
(iii)72﹣4×32=13 ③
…
根据上述规律解决下列问题:
(1)完成第五个等式:112﹣4× 2=;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,属于假命题的是( )
A. 三角形的内角和等于180°; B. 圆是轴对称图形,任何一条直径都是圆的对称轴;
C. 对顶角相等; D. 在同一平面内,垂直于同一条直线的两条直线相互平行.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com