
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 交于A(1,﹣3),B(a,﹣1)两点.
交于A(1,﹣3),B(a,﹣1)两点.
(1)求一次函数的解析式;
(2)根据反比例函数![]() 的图象,当y>6时,求出x的取值范围;
的图象,当y>6时,求出x的取值范围;
(3)若一次函数![]() 与反比例函数
与反比例函数![]() 有一个交点,求c的值.
有一个交点,求c的值.
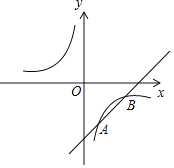
【答案】(1)一次函数的解析式为y=x﹣4;
(2)x的取值范围为﹣![]() <x<0;
<x<0;
(3)c=±2![]()
【解析】试题分析:(1)将A代入反比例函数即可求出m的值,将B代入反比例函数即可求出a的值,然后将A、B两点代入一次函数即可求出k与b的值.
(2)令y=6代入反比例函数解析式中求出x的值,根据图象即可求出x的范围;
(3)一次函数为y=x+c,由于一次函数与反比例函数只有一个交点,所以联立方程可知△=0,解方程后即可求出c的值.
试题解析:
(1)将A(1,﹣3)代入y=![]() ,
,
∴m=﹣3,
∴反比例函数的解析式为:y=﹣![]() ,
,
将B(a,﹣1)代入y=﹣![]() ,
,
∴a=3,
将A(1,﹣3)和B(3,﹣1)代入y=kx+b,
∴解得![]() ,
,
∴一次函数的解析式为y=x﹣4;
(2)令y=6代入y=-![]() ,
,
∴x=﹣![]() ,
,
∴当y>6时,
根据图象可知:x的取值范围为﹣![]() <x<0;
<x<0;
(3)由于k=1,
∴y=x+c,
联立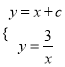 ,
,
化简可得:x2+cx+3=0,
∴△=c2﹣12=0,
∴c=±2![]()


科目:初中数学 来源: 题型:
【题目】甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶, 快递车到达乙地后,卸完物资并另装货物共用了 45 分钟,然后按原路以另一速度返回,直至与货车相遇.已知货车行驶速度为 60 km/h,两车间的距离 y(km) 与货车行驶时间 x(h) 之间的函数图象如图所示:
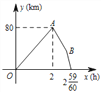
给出以下四个结论:
① 快递车从甲地到乙地的速度是 100 km/h;
② 甲、乙两地之间的距离是 80 km;
③ 图中点 B 的坐标为 (![]() , 35);
, 35);
④ 快递车从乙地返回时的速度为 90 km/h.
其中正确的是_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线. 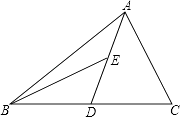
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为40,BD=5,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚硬币,正面一定朝上
B.某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖
C.旅客上飞机前的安检应采用抽样调查
D.方差越大,数据的波动越大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.3个人分成两组,并且每组必有人,一定有2个人分在一组
B.抛一枚硬币,正面朝上
C.随意掷两个均匀的骰子,朝上面的点数之和为6
D.打开电视,正在播放动画片
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com