
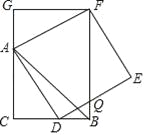
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,其中正确的结论的个数是_____.
【答案】①②③④ .
【解析】
由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;
证明四边形CBFG是矩形,得出S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;
证出△ACD∽△FEQ,得出对应边成比例,得出④正确.
解:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,
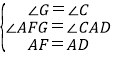 ,
,
∴△FGA≌△ACD(AAS),
∴AC=FG,①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,③正确;
∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴ADFE=AD2=FQAC,④正确;
故答案为:①②③④.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的
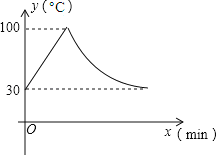
A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ ![]() PB.
PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
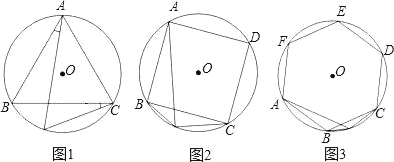
查看答案和解析>>
科目:初中数学 来源: 题型:
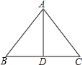
【题目】如图,在![]() 中,
中,![]() 为直线
为直线![]() 上任意一点,给出以下判断:
上任意一点,给出以下判断:
①若点![]() 到
到![]() ,
,![]() 距离相等,且
距离相等,且![]() ,则
,则![]() ;②若
;②若![]() 且
且![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,且
,且![]() ,则
,则![]() .其中正确的是________(把所有正确结论序号都填在横线上)
.其中正确的是________(把所有正确结论序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
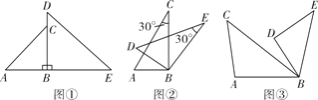
【题目】△ABC和△DBE是绕点B旋转的两个相似三角形,其中∠ABC与∠DBE、∠A与∠D为对应角.
(1)如图①,若△ABC和△DBE分别是以∠ABC与∠DBE为顶角的等腰直角三角形,且两三角形旋转到使点B、C、D在同一条直线上的位置时,请直接写出线段AD与线段EC的关系;
(2)若△ABC和△DBE为含有30°角的直角三角形,且两个三角形旋转到如图②的位置时,试确定线段AD与线段EC的关系,并说明理由;
(3)若△ABC和△DBE为如图③的两个三角形,且∠ACB=α,∠BDE=β,在绕点B旋转的过程中,直线AD与EC夹角的度数是否改变?若不改变,直接用含α、β的式子表示夹角的度数;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
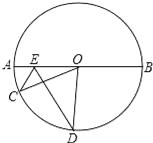
【题目】如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),且∠CED=∠OED=60°,连OC、OD
(1)求证:∠C=∠D;
(2)若⊙O的半径为r,请直接写出CE+ED的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
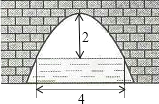
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
A.3 B.2![]() C.3
C.3![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=5,BC=3.
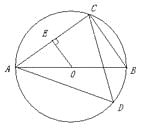
(1) 求sin∠BAC的值;
(2) 如果OE⊥AC, 垂足为E,求OE的长;
(3) 求tan∠ADC的值.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com