
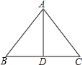
【题目】如图,在![]() 中,
中,![]() 为直线
为直线![]() 上任意一点,给出以下判断:
上任意一点,给出以下判断:
①若点![]() 到
到![]() ,
,![]() 距离相等,且
距离相等,且![]() ,则
,则![]() ;②若
;②若![]() 且
且![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,且
,且![]() ,则
,则![]() .其中正确的是________(把所有正确结论序号都填在横线上)
.其中正确的是________(把所有正确结论序号都填在横线上)
【答案】①②④
【解析】
①如图1,过D作DE⊥AB于E,DF⊥AC于F,通过证明Rt△BDE≌Rt△CDF,得到∠B=∠C,即可得到结论;
②由垂直的定义得到∠ADB=∠ADC=90°,由AD2=BDDC,得到![]() ,证得△ABD∽△ACD,根据相似三角形的性质得到∠BAD=∠C,即可得到结论;
,证得△ABD∽△ACD,根据相似三角形的性质得到∠BAD=∠C,即可得到结论;
③作AE⊥BC于E,根据勾股定理得到AB2=AE2+BE2,AD2=AE2+DE2,再两式相减即可求解;
④利用等角的余角相等得到∠B=∠DAC,则可判断Rt△ADB∽Rt△CDA,所以AD:CD=BD:AD,然后根据比例的性质即可得到结论.

解:①图1,过D作DE⊥AB于E,DF⊥AC于F,
∵点D到AB,AC距离相等,
∴DE=DF,
在Rt△BDE与Rt△CDF中,![]() ,
,
∴Rt△BDE≌Rt△CDF,
∴∠B=∠C,
∴AB=AC; ①正确
②AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AD2=BDDC,
∴![]() ,
,
∴△ABD∽△ACD,
∴∠BAD=∠C,
∵∠B+∠BAD=90°,
∴∠C+∠B=90°,
∴∠BAC=90°; ②正确
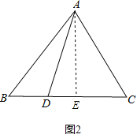
③如图2,作AE⊥BC于E,则
AB2=AE2+BE2,AD2=AE2+DE2,
则AB2-AD2=(AE2+BE2)-(AE2+DE2)=BE2-DE2=(BE+DE)(BE-DE)=BDDC,
则AD2+BDDC=AB2,
∵AB=AC,
∴AD2+BDDC=AC2;
如图3,作AE⊥BC于E,则
AB2=AE2+BE2,AD2=AE2+DE2,
则AD2-AB2=(AE2+DE2)-(AE2+BE2)=DE2-BE2=(BE+DE)(DE-BE)=BDDC,
则AD2-BDDC=AB2,
∵AB=AC,
∴AD2-BDDC=AC2;故③错误;
④∵AD⊥BC于点D,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
∵∠BAD=∠DAC=90°,
∴∠B=∠DAC,
∴Rt△ADB∽Rt△CDA,
∴AD:CD=BD:AD,
∴AD2=CDBD.④正确
故答案为:①②④.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? (填“是”或“否”),∠BOE= 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
(2)如图c,在AB和AC上分别截取点B′和C′,使AB=![]() AB′,AC=
AB′,AC=![]() AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有 4 个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率
(2)随机摸出两个小球,直接写出“两次取出的球标号和等于 4”的概率.
(3)梯形ABCD中,AB∥DC,∠B=90°,E 为直线 BC上一点,若AB=5,BC=12,DC=7,当BE=?时,△ABE与△DEC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
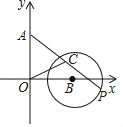
A. 1 B. 2![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点E.
求证:(1)DE⊥AE;
(2)AE+CE=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
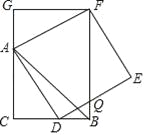
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,其中正确的结论的个数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
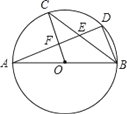
A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
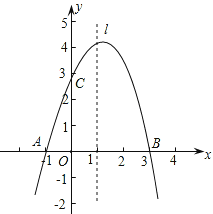
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在左边托盘A(固定)中放置一个生物,在右边托盘B(可左右移动)中放置一定重量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的跳高,记录相应的托盘B中的砝码质量,得到下表:
托盘B与点M的距离x(cm) | 10 | 15 | 20 | 25 | 30 |
托盘B中的砝码质量y(g) | 30 | 20 | 15 | 12 | 10 |
(1)把上表中(x,y)的各级对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑的曲线连接起来,观察所画的图象,猜想y与x的函数关系,求出该函数关系式.
(2)当托盘B向左移动(不能超过点M)时,应往托盘B中添加砝码还是减少砝码?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com