
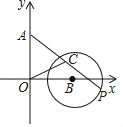
【题目】如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A. 1 B. 2![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]() ﹣1
﹣1
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(6分)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).

(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=BC=2,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD是它的角平分线.
(1)如图1,求证:S△ABD:S△ACD=AB:AC=BD:CD;
(2)如图2,E是AB上的点,连接ED,若BD=3,BE=CD=2,AE=2CD,求证:△BED是等腰三角形;
(3)在图1中,若3∠BAC=2∠C,∠ADB>∠B>∠BAD,直接写出∠BAC的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有长度分别为3cm、4cm、5cm、8cm的4根木条
(1)李鑫同学从中任取一根,抽到“长度是4cm的木条”的概率是 .
(2)在李鑫同学取出4cm的木条后,王华同学又从剩下的木条中,同时随机取出两根,求他们取出的三根木条能构成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
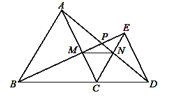
【题目】如图,△ABC和△CDE都是等边三角形,B,C,D三点在一条直线上,AD与BE交于点P,AC,BE交于点M,AD,CE交于点N,连接MN,则下列五个结论:①AD=BE;②∠BMC=∠ANE;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中一定正确的是__________.(填出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
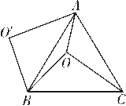
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;&
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AOBO′的面积为6+3![]() ;
;
⑤S△AOC+S△AOB=6+![]() .
.
其中正确的结论是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
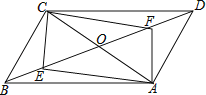
【题目】如图,在平行四边形ABCD中,AC,BD相交于点O,AC=6,BD=8,∠AOD=65°,点E在BO上,AF∥CE交BD于点F.
(1)求证:四边形AFCE是平行四边形.
(2)当点E在边BO上移动时,平行四边形AFCE能否为矩形?若能,此时BE的长为多少(直接写出结果)?若不能,请说明理由.
(3)当点E在边BO上移动时,平行四边形AFCE能否为菱形?若能,此时BE的长为多少(直接写出结果)?若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com