
【题目】在△ABC中,AD是它的角平分线.
(1)如图1,求证:S△ABD:S△ACD=AB:AC=BD:CD;
(2)如图2,E是AB上的点,连接ED,若BD=3,BE=CD=2,AE=2CD,求证:△BED是等腰三角形;
(3)在图1中,若3∠BAC=2∠C,∠ADB>∠B>∠BAD,直接写出∠BAC的取值范围 .

【答案】(1)证明见解析;(2)证明见解析;(3)40°<∠BAC<60°.
【解析】
(1)作辅助线,构建三角形的性质得:DE=DF,利用三角形面积的不同计算方法可得结论;
(2)证明△AED≌△ACD,可得DE=CD=BE,可得结论;
(3)设∠BAD=x,根据∠ADB>∠B>∠BAD,列不等式可解答.
证明:(1)如图1,过D作DE⊥AB于E,DF⊥AC于F,

∵AD平分∠BAC,
∴DE=DF,
∴![]() =
=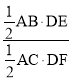 =
=![]() =
=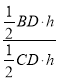 =
=![]() ;
;
S△ABD:S△ACD=AB:AC=BD:CD;
(2)如图2,由(1)知:AB:AC=BD:CD;
∵BE=CD=2,AE=2CD=4,
∴![]() ,AC=4=AE,
,AC=4=AE,
在△AED和△ACD中
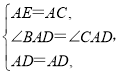
∴△AED≌△ACD(SAS),
∴ED=CD=2,
∵BE=2,∴BE=DE=2,
∴△BED是等腰三角形;
(3)设∠BAD=x,则∠BAC=2x,
∵3∠BAC=2∠C,
∴∠C=3x,
∴∠ADB=∠DAC+∠C=4x,
∵∠ADB>∠B>∠BAD,
∴4x>1805x>x,
解得:20°<x<30°,
∴40°<∠BAC<60°.
故答案为:40°<∠BAC<60°.


科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=![]() OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() 满足下列条件:①抛物线y=ax2+bx与直线y=x只有一个交点;②对于任意实数x,a(-x+5)2+b(-x+5)=a(x-3)2+b(x-3)都成立.
满足下列条件:①抛物线y=ax2+bx与直线y=x只有一个交点;②对于任意实数x,a(-x+5)2+b(-x+5)=a(x-3)2+b(x-3)都成立.
(1)求二次函数y=ax2+bx的解析式;
(2)若当-2≤x≤r(r≠0)时,恰有t≤y≤1.5r成立,求t和r的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
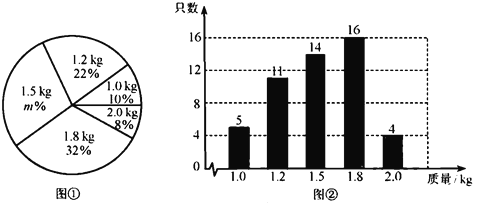
(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F
(1)求证:△DAC≌△EAB;
(2)若∠AEF=15°,EF=4,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
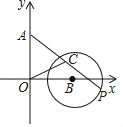
【题目】如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A. 1 B. 2![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
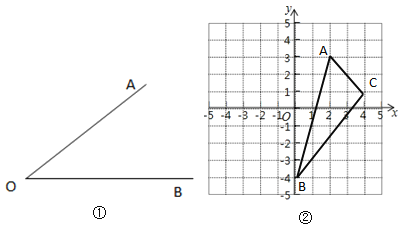
(1)如图①,已知:![]() .求作:射线
.求作:射线![]() ,使
,使![]() 平分
平分![]() .(要求:尺规作图,不写作法,但需保留作图痕迹) .
.(要求:尺规作图,不写作法,但需保留作图痕迹) .
(2)题(1)中作图的依据是全等三角形判定方法中的__________.
(3)在图②中作出![]() ,使它与
,使它与![]() 关于
关于![]() 轴对称.
轴对称.
(4)在图②中的![]() 轴上找到一点
轴上找到一点![]() ,使
,使![]() 的周长最小.
的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
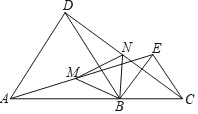
【题目】如图,点A、B、C在同一直线上,△ABD,△BCE都是等边三角形.
(1)求证:AE=CD;
(2)若M,N分别是AE,CD的中点,试判断△BMN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①是一个重要公式的几何解释.请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B、C、D三点在一条直线上.试证明∠ACE=90°;
(3)伽菲尔德(G a rfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com