
【题目】作图题:
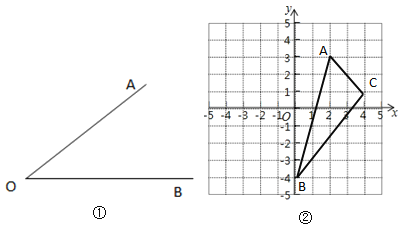
(1)如图①,已知:![]() .求作:射线
.求作:射线![]() ,使
,使![]() 平分
平分![]() .(要求:尺规作图,不写作法,但需保留作图痕迹) .
.(要求:尺规作图,不写作法,但需保留作图痕迹) .
(2)题(1)中作图的依据是全等三角形判定方法中的__________.
(3)在图②中作出![]() ,使它与
,使它与![]() 关于
关于![]() 轴对称.
轴对称.
(4)在图②中的![]() 轴上找到一点
轴上找到一点![]() ,使
,使![]() 的周长最小.
的周长最小.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且![]() .连接PB,试探究PA,PB,PC满足的等量关系.
.连接PB,试探究PA,PB,PC满足的等量关系.

图1 图2
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到![]() ,连接
,连接![]() ,如图1所示.
,如图1所示.
由![]() ≌
≌![]() 可以证得
可以证得![]() 是等边三角形,再由
是等边三角形,再由![]() 可得∠APC的大小为 度,进而得到
可得∠APC的大小为 度,进而得到![]() 是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
是直角三角形,这样可以得到PA,PB,PC满足的等量关系为 ;
(2)如图2,当α=120°时,请参考(1)中的方法,探究PA,PB,PC满足的等量关系,并给出证明;
(3)PA,PB,PC满足的等量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E为正方形ABCD的边AD上一点,连接BE,过点C作CN⊥BE,垂足为M,交AB于点N.
(1)求证:△ABE≌△BCN;
(2)若N为AB的中点,求tan∠ABE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD是它的角平分线.
(1)如图1,求证:S△ABD:S△ACD=AB:AC=BD:CD;
(2)如图2,E是AB上的点,连接ED,若BD=3,BE=CD=2,AE=2CD,求证:△BED是等腰三角形;
(3)在图1中,若3∠BAC=2∠C,∠ADB>∠B>∠BAD,直接写出∠BAC的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
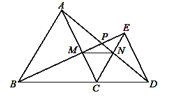
【题目】如图,△ABC和△CDE都是等边三角形,B,C,D三点在一条直线上,AD与BE交于点P,AC,BE交于点M,AD,CE交于点N,连接MN,则下列五个结论:①AD=BE;②∠BMC=∠ANE;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中一定正确的是__________.(填出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
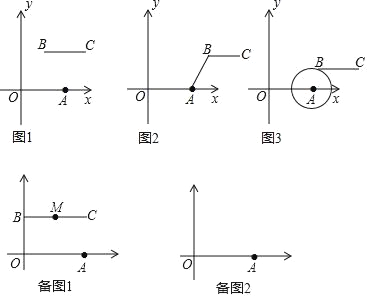
【题目】定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
(1)根据上述定义,当m=2,n=3时,如图1,线段BC与线段OA的距离是 ,当m=5,n=3时,如图2,线段BC与线段OA的距离(即线段AB的长)为 .
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
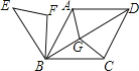
【题目】如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,G为对角线BD(不含B点)上任意一点,将△ABG绕点B逆时针旋转60°得到△EBF,当AG+BG+CG取最小值时EF的长( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
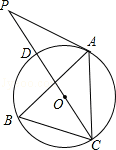
【题目】如图,点A.B.C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com