
【题目】定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
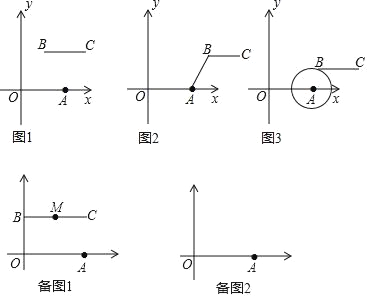
(1)根据上述定义,当m=2,n=3时,如图1,线段BC与线段OA的距离是 ,当m=5,n=3时,如图2,线段BC与线段OA的距离(即线段AB的长)为 .
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)3,![]() ;(2)d=
;(2)d=![]() ;(3)存在m的值使以A、M、H为顶点的三角形与△AOD相似,m的取值为:1、3或
;(3)存在m的值使以A、M、H为顶点的三角形与△AOD相似,m的取值为:1、3或![]() .
.
【解析】
(1)理解新定义,按照新定义的要求求出两个距离值;
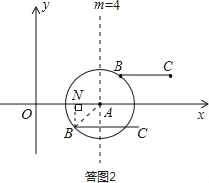
(2)如答图2所示,当点B落在⊙A上时,m的取值范围为2≤m≤6:
当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;
当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长;
(3)如答图4所示,符合题意的相似三角形有三个,需要进行分类讨论,分别利用点的坐标关系以及相似三角形比例线段关系求出m的值.
(1)当m=2,n=3时,
如题图1,线段BC与线段OA的距离(即平行线BC与OA之间的距离)=3;
当m=5,n=3时,
B点坐标为(5,3),线段BC与线段OA的距离,即为线段AB的长,
如答图1,过点B作BN⊥x轴于点N,则AN=1,BN=3,
在Rt△ABN中,由勾股定理得:AB=![]() =
=![]() =
=![]() .
.
故答案为3,![]()
(2)如答图2所示,当点B落在⊙A上时,m的取值范围为2≤m≤6:
当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;
当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长,
ON=m,AN=OA﹣ON=4﹣m,在Rt△ABN中,由勾股定理得:
∴d=![]() =
=![]() .
.
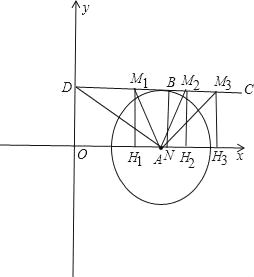
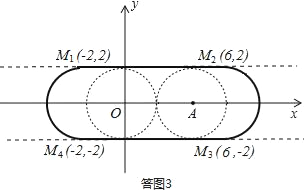
(3)①依题意画出图形,点M的运动轨迹如答图3中粗体实线所示:
由图可见,封闭图形由上下两段长度为8的线段,以及左右两侧半径为2的半圆所组成,
其周长为:2×8+2×π×2=16+4π,
∴点M随线段BC运动所围成的封闭图形的周长为:16+4π.
②结论:存在.
∵m≥0,n≥0,∴点M位于第一象限.
∵A(4,0),D(0,2),∴OA=2OD.
如答图4所示,相似三角形有三种情形:
(I)△AM1H1,此时点M纵坐标为2,点H在A点左侧.
如图,OH1=m+2,M1H1=2,AH1=OA﹣OH1=2﹣m,
由相似关系可知,M1H1=2AH1,即2=2(2﹣m),
∴m=1;
(II)△AM2H2,此时点M纵坐标为2,点H在A点右侧.
如图,OH2=m+2,M2H2=2,AH2=OH2﹣OA=m﹣2,
由相似关系可知,M2H2=2AH2,即2=2(m﹣2),
∴m=3;
(III)△AM3H3,此时点B落在⊙A上.
如图,OH3=m+2,AH3=OH3﹣OA=m﹣2,
过点B作BN⊥x轴于点N,则BN=M3H3=n,AN=m﹣4,
由相似关系可知,AH3=2M3H3,即m﹣2=2n (1)
在Rt△ABN中,由勾股定理得:22=(m﹣4)2+n2 (2)
由(1)、(2)式解得:m1=![]() ,m2=2,
,m2=2,
当m=2时,点M与点A横坐标相同,点H与点A重合,故舍去,
∴m=![]() .
.
综上所述,存在m的值使以A、M、H为顶点的三角形与△AOD相似,m的取值为:1、3或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
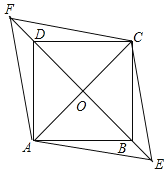
(1)求证:四边形AECF是菱形;
(2)若AC=4,BE=1,求菱形AECF的边长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F
(1)求证:△DAC≌△EAB;
(2)若∠AEF=15°,EF=4,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
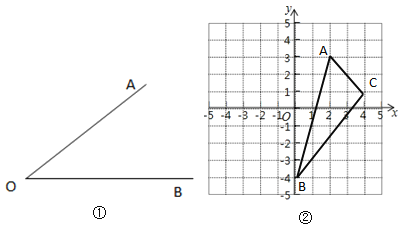
(1)如图①,已知:![]() .求作:射线
.求作:射线![]() ,使
,使![]() 平分
平分![]() .(要求:尺规作图,不写作法,但需保留作图痕迹) .
.(要求:尺规作图,不写作法,但需保留作图痕迹) .
(2)题(1)中作图的依据是全等三角形判定方法中的__________.
(3)在图②中作出![]() ,使它与
,使它与![]() 关于
关于![]() 轴对称.
轴对称.
(4)在图②中的![]() 轴上找到一点
轴上找到一点![]() ,使
,使![]() 的周长最小.
的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
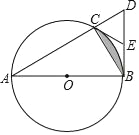
【题目】如图,已知△ABC内接于⊙O,A B为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)E为BD的中点,连结CE,求证:CE是⊙O的切线.
(2)若AC=3,CD=1,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
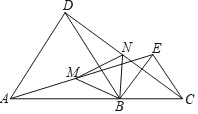
【题目】如图,点A、B、C在同一直线上,△ABD,△BCE都是等边三角形.
(1)求证:AE=CD;
(2)若M,N分别是AE,CD的中点,试判断△BMN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.
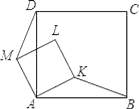
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,4),C(8,0).
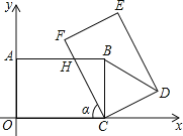
(1)当α=60°时,△CBD的形状是______;
(2)设AH=m
①连接HD,当△CHD的面积等于10时,求m的值;
②当0°<α<90°旋转过程中,连接OH,当△OHC为等腰三角形时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.
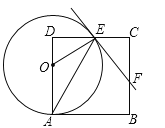
(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com