
【题目】如图,点A、B、C在同一直线上,△ABD,△BCE都是等边三角形.
(1)求证:AE=CD;
(2)若M,N分别是AE,CD的中点,试判断△BMN的形状,并证明你的结论.
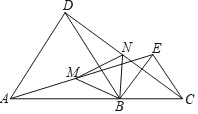
【答案】(1)答案见解析;(2)△MBN是等边三角形.
【解析】整体分析:
(1)利用SAS证明△AOC≌△BOD,则有AE=CD;(2)由△ABE≌△DBC,可证△ABM≌△DBN,从而得BM=BN,∠MBN=60°.
(1)证明:∵△ABD、△BCE都是等边三角形,
∴AB=BD,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠DBE=∠DBE+∠CBE即∠ABE=∠DBC,
∴在△ABE和△DBC中,
△ABE≌△DBC(SAS).
∴AE=CD.
(2)解:△MBN是等边三角形,理由如下:
∵△ABE≌△DBC,
∴∠BAE=∠BDC.
∵AE=CD,M、N分别是AE、CD的中点,
∴AM=DN;
又∵AB=DB.
∴△ABM≌△DBN.
BM=BN.
∠ABM=∠DBN.
∴∠DBM+∠DBN=∠DBM+∠ABM=∠ABD=60°.
∴△MBN是等边三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题14分)如图①,已知抛物线![]() (a≠0)与
(a≠0)与![]() 轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
轴交于点A(1,0)和点B(-3,0),与y轴交于点C.

(1)求抛物线的解析式;
(2)设抛物线的对称轴与![]() 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)如图1,请你写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点O,连接AP,BO.猜想并写出BO与AP所满足的数量关系和位置关系,并说明理由;
(3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明理由.
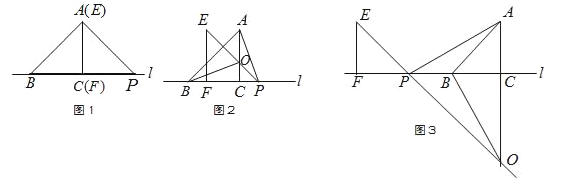
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由方程3x-5=2x-4变形,得3x-2x=-4+5,这是根据什么变形的( )
A. 合并同类项法则B. 分配律C. 等式的基本性质1D. 等式的基本性质2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com