【题目】已知点E为正方形ABCD的边AD上一点，连接BE，过点C作CN⊥BE，垂足为M，交AB于点N．
（1）求证：△ABE≌△BCN；
（2）若N为AB的中点，求tan∠ABE．
【答案】（1）证明见解析；（2）
【解析】
（1）根据正方形的性质得到AB＝BC，∠A＝∠CBN＝90°，∠1＋∠2＝90°，根据垂线和三角形内角和定理得到∠2＋∠3＝90°，推出∠1＝∠3，根据ASA推出△ABE≌△BCN；（2）tan∠ABE＝
，根据已知求出AE与AB的关系即可求得tan∠ABE.
（1）证明：∵四边形ABCD为正方形
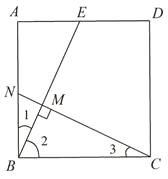
∴AB=BC，∠A=∠CBN=90°，∠1+∠2=90°
∵CM⊥BE，
∴∠2+∠3=90°
∴∠1=∠3
在△ABE和△BCN中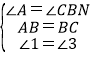
，
∴△ABE≌△BCN（ASA）；
（2）∵N为AB中点，
∴BN=AB
又∵△ABE≌△BCN，
∴AE=BN=AB
在Rt△ABE中，tan∠ABE═
．
科目：初中数学 来源： 题型：
【题目】已知:1号探测气球从海拔5m处匀速上升，同时，2号探测气球从海拔15m处匀速上升，且两个气球都上升了1h．两个气球所在位置的海拔y(单位：m)与上升时间x(单位：min)之间的函数关系如图所示，根据图中的信息，下列说法：
①上升20min时，两个气球都位于海拔25m的高度；
②1号探测气球所在位置的海拔关于上升时间x的函数关系式是y=x+5(0≤x≤60)；
③记两个气球的海拔高度差为m，则当0≤x≤50时，m的最大值为15m．
其中，说法正确的个数是（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的对角线AC，BD相交于点O，将BD向两个方向延长，分别至点E和点F，且使BE＝DF．
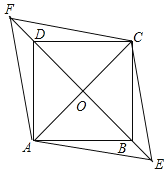
（1）求证：四边形AECF是菱形；
（2）若AC＝4，BE＝1，求菱形AECF的边长和面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：二次函数
满足下列条件：①抛物线y=ax2+bx与直线y=x只有一个交点；②对于任意实数x，a（-x+5）2+b（-x+5）=a（x-3）2+b（x-3）都成立．
（1）求二次函数y=ax2+bx的解析式；
（2）若当-2≤x≤r（r≠0）时，恰有t≤y≤1.5r成立，求t和r的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
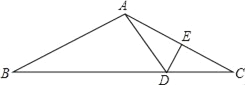
【题目】如图，在△ABC中，AB=AC，AC的垂直平分线分别交BC、AC于点D、E．
（1）若AC=12，BC=15，求△ABD的周长；
（2）若∠B=20°，求∠BAD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡，根据它们的质量（单位：
），绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：
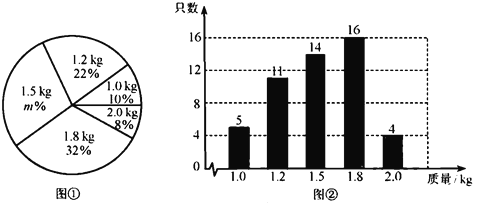
（Ⅰ）图①中
的值为 ；
（Ⅱ）求统计的这组数据的平均数、众数和中位数；
（Ⅲ） 根据样本数据，估计这2500只鸡中，质量为
的约有多少只？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，等腰Rt△ABC，等腰Rt△ADE，AB⊥AC，AD⊥AE，AB=AC，AD=AE，CD交AE、BE分别于点M、F
（1）求证：△DAC≌△EAB；
（2）若∠AEF=15°，EF=4，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】作图题:
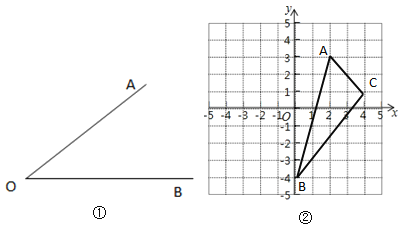
（1）如图①，已知：
．求作：射线
，使平分．(要求：尺规作图，不写作法，但需保留作图痕迹) ．
（2）题（1）中作图的依据是全等三角形判定方法中的__________．
（3）在图②中作出
，使它与
关于
轴对称．
（4）在图②中的
轴上找到一点
，使
的周长最小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，把矩形COAB绕点C顺时针旋转α角，得到矩形CFED．设FC与AB交于点H，且A（0，4），C（8，0）．
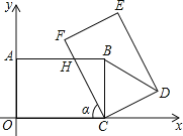
（1）当α=60°时，△CBD的形状是______；
（2）设AH=m
①连接HD，当△CHD的面积等于10时，求m的值；
②当0°＜α＜90°旋转过程中，连接OH，当△OHC为等腰三角形时，请直接写出m的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com