
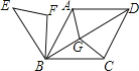
【题目】如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,G为对角线BD(不含B点)上任意一点,将△ABG绕点B逆时针旋转60°得到△EBF,当AG+BG+CG取最小值时EF的长( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据“两点之间线段最短”,当G点位于BD与CE的交点处时,AG+BG+CG的值最小,即等于EC的长.
解:如图,
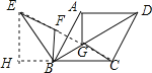
∵将△ABG绕点B逆时针旋转60°得到△EBF,
∴BE=AB=BC,BF=BG,EF=AG,
∴△BFG是等边三角形.
∴BF=BG=FG,.
∴AG+BG+CG=FE+GF+CG.
根据“两点之间线段最短”,
∴当G点位于BD与CE的交点处时,AG+BG+CG的值最小,即等于EC的长,
过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=180°-120°=60°,
∵BC=4,
∴BF=2,EF=2![]() ,在Rt△EFC中,
,在Rt△EFC中,
∵EF2+FC2=EC2,
∴EC=4![]() .
.
∵∠CBE=120°,
∴∠BEF=30°,
∵∠EBF=∠ABG=30°,
∴EF=BF=FG,
∴EF=![]() CE=
CE=![]() ,
,
故选:D.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() 满足下列条件:①抛物线y=ax2+bx与直线y=x只有一个交点;②对于任意实数x,a(-x+5)2+b(-x+5)=a(x-3)2+b(x-3)都成立.
满足下列条件:①抛物线y=ax2+bx与直线y=x只有一个交点;②对于任意实数x,a(-x+5)2+b(-x+5)=a(x-3)2+b(x-3)都成立.
(1)求二次函数y=ax2+bx的解析式;
(2)若当-2≤x≤r(r≠0)时,恰有t≤y≤1.5r成立,求t和r的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
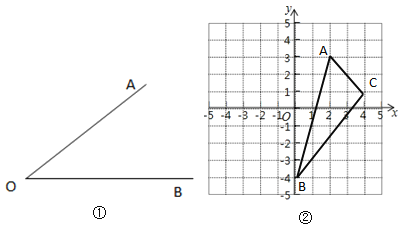
(1)如图①,已知:![]() .求作:射线
.求作:射线![]() ,使
,使![]() 平分
平分![]() .(要求:尺规作图,不写作法,但需保留作图痕迹) .
.(要求:尺规作图,不写作法,但需保留作图痕迹) .
(2)题(1)中作图的依据是全等三角形判定方法中的__________.
(3)在图②中作出![]() ,使它与
,使它与![]() 关于
关于![]() 轴对称.
轴对称.
(4)在图②中的![]() 轴上找到一点
轴上找到一点![]() ,使
,使![]() 的周长最小.
的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
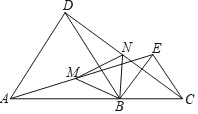
【题目】如图,点A、B、C在同一直线上,△ABD,△BCE都是等边三角形.
(1)求证:AE=CD;
(2)若M,N分别是AE,CD的中点,试判断△BMN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
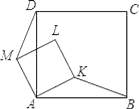
【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,4),C(8,0).
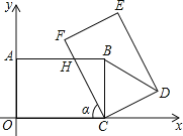
(1)当α=60°时,△CBD的形状是______;
(2)设AH=m
①连接HD,当△CHD的面积等于10时,求m的值;
②当0°<α<90°旋转过程中,连接OH,当△OHC为等腰三角形时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①是一个重要公式的几何解释.请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B、C、D三点在一条直线上.试证明∠ACE=90°;
(3)伽菲尔德(G a rfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
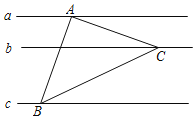
【题目】在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,则△ABC的面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com