
【题目】在![]() 中,
中,![]() ,边AB的垂直平分线交边BC于点D,边AC的垂直平分线交边BC于点E,连结AD,AE,则
,边AB的垂直平分线交边BC于点D,边AC的垂直平分线交边BC于点E,连结AD,AE,则![]() 的度数为______
的度数为______![]() 用含
用含![]() 的代数式表示
的代数式表示![]()
【答案】2α﹣180°或180°﹣2α
【解析】
分两种情况进行讨论,先根据线段垂直平分线的性质,得到∠B=∠BAD,∠C=∠CAE,进而得到∠BAD+∠CAE=∠B+∠C=180°-![]() ,再根据角的和差关系进行计算即可.
,再根据角的和差关系进行计算即可.
解:有两种情况:
①如图所示,当∠BAC90°时,
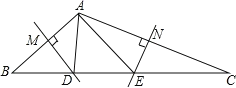
∵DM垂直平分AB,
∴DA=DB,
∴∠B=∠BAD,
同理可得,∠C=∠CAE,
∴∠BAD+∠CAE=∠B+∠C=180°α,
∴∠DAE=∠BAC(∠BAD+∠CAE)=α(180°α)=2α180°;
②如图所示,当∠BAC<90°时,
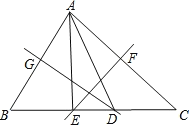
∵DM垂直平分AB,
∴DA=DB,
∴∠B=∠BAD,
同理可得,∠C=∠CAE,
∴∠BAD+∠CAE=∠B+∠C=180°α,
∴∠DAE=∠BAD+∠CAE∠BAC=180°αα=180°2α.
故答案为:2α180°或180°2α.


科目:初中数学 来源: 题型:
【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程![]() (千米)与时间
(千米)与时间![]() (分钟)的关系,请根据图象提供的信息回答问题:
(分钟)的关系,请根据图象提供的信息回答问题:

(1)![]() 和
和![]() 中,__________描述小凡的运过程.
中,__________描述小凡的运过程.
(2)___________谁先出发,先出发了___________分钟.
(3)___________先到达图书馆,先到了____________分钟.
(4)当![]() _________分钟时,小凡与小光在去学校的路上相遇.
_________分钟时,小凡与小光在去学校的路上相遇.
(5)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某某摩托车厂本周计划每日生产![]() 辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量,与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量,与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
根据记录回答:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)本周三生产了多少摩托车?
(2)本周总生产量与计划生产量相比,是增加还是减少?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点![]() 、
、![]() ,则线段AB的中点坐标可以表示为
,则线段AB的中点坐标可以表示为![]()

(简单应用)如图1,直线AB与y轴交于点![]() ,与x轴交于点
,与x轴交于点![]() ,过原点O的直线L将
,过原点O的直线L将![]() 分成面积相等的两部分,请求出直线L的解析式;
分成面积相等的两部分,请求出直线L的解析式;
(探究升级)小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”
如图2,在四边形ABCD中,对角线AC、BD相交于点O,![]() 试说明
试说明![]() ;
;
(综合运用)如图3,在平面直角坐标系中![]() ,
,![]() ,
,![]() ,若OC恰好平分四边形OACB的面积,求点C的坐标.
,若OC恰好平分四边形OACB的面积,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从甲、乙两个跳远运动员中选一人参加一项比赛,在最近的10次选拨赛中,他们的成绩![]() 单位:
单位:![]() 如下:
如下:
甲:585,596,610,598,612,597,604,600,613,601
乙:613,618,580,574,618,593,585,590,598,624
![]() 分别求甲、乙的平均成绩;
分别求甲、乙的平均成绩;
![]() 分别求甲、乙这十次成绩的方差;
分别求甲、乙这十次成绩的方差;
![]() 这两名运动员的运动成绩各有什么特点?历届比赛成绩表明,成绩达到
这两名运动员的运动成绩各有什么特点?历届比赛成绩表明,成绩达到![]() 就很可能夺冠你认为应选谁参加比赛?
就很可能夺冠你认为应选谁参加比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,已知
,已知![]() ,点
,点![]() ,
, ![]() 分别是射线
分别是射线![]() ,
, ![]() 上两定点,且
上两定点,且![]() ,
, ![]() ;动点
;动点![]() 从点
从点![]() 向点
向点![]() 运动,以
运动,以![]() 为斜边向右侧作等腰直角
为斜边向右侧作等腰直角![]() .设线段
.设线段![]() 的长
的长![]() ,点
,点![]() 到射线
到射线![]() 的距离为
的距离为![]() .
.
(1)若![]() ,直接写出点
,直接写出点![]() 到射线
到射线![]() 的距离;
的距离;
(2)求![]() 关于
关于![]() 的函数表达式,并在图
的函数表达式,并在图![]() 中画出函数图象;
中画出函数图象;
(3)当动点![]() 从点
从点![]() 运动到点
运动到点![]() ,求点
,求点![]() 运动经过的路径长.
运动经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a﹣c|=10,|a﹣d|=12,|b﹣d|=9,则|b﹣c|= . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣4,5),C(﹣3,0).将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A'B'C',其中点A',B',分别为点A,B,C的对应点.
(1)请在所给坐标系中画出△A'B'C',并直接写出点C'的坐标;
(2)若AB边上一点P经过上述平移后的对应点为P'(x,y),用含x,y的式子表示点P的坐标;(直接写出结果即可)
(3)求△A'B'C'的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com