
【题目】如图,在平行四边形ABCD中,AC,BD相交于点O,AC=6,BD=8,∠AOD=65°,点E在BO上,AF∥CE交BD于点F.
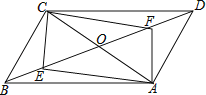
(1)求证:四边形AFCE是平行四边形.
(2)当点E在边BO上移动时,平行四边形AFCE能否为矩形?若能,此时BE的长为多少(直接写出结果)?若不能,请说明理由.
(3)当点E在边BO上移动时,平行四边形AFCE能否为菱形?若能,此时BE的长为多少(直接写出结果)?若不能,请说明理由.
【答案】(1)见解析;(2)平行四边形AFCE能为矩形,此时BE=1;(3)平行四边形AFCE不能为菱形,理由见解析.
【解析】
(1)四边形ABCD为平行四边形,又AF∥CE,易证得△AOF≌△COE,则可得OE=OF,又由OA=OC,即可判定四边形AFCE是平行四边形;
(2)当EF=AC时,平行四边形AFCE为矩形,先得出BE=DF,再由AC=EF=6,BD=8,即可求得此时BE的长;
(3)由∠AOD=65°,可得AC与BD不垂直,即可得平行四边形AFCE不能为菱形.
(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AF∥CE,
∴∠OAF=∠OCE,
在△AOF和△COE中,
 ,
,
∴△AOF≌△COE(ASA),
∴OE=OF,又OA=OC,
∴四边形AFCE是平行四边形;
(2)解:平行四边形AFCE能为矩形.
理由:∵四边形AFCE是平行四边形,
∴当EF=AC=6时,平行四边形AFCE为矩形,
∴OE=OF,又OB=OD,
∴BE=DF,
∴2BE+EF=BD,
即2BE+6=8,
解得:BE=1,
∴当BE=1时,平行四边形AFCE为矩形;
(3)解:平行四边形AFCE不能为菱形.
理由:∵四边形AFCE是平行四边形,且∠AOD=65°,
即AC与BD不垂直,
∴平行四边形AFCE不能为菱形.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
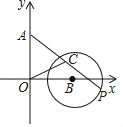
A. 1 B. 2![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;

(2)补全条形统计图;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①是一个重要公式的几何解释.请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B、C、D三点在一条直线上.试证明∠ACE=90°;
(3)伽菲尔德(G a rfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC 是等腰直角三角形,∠ABC=90°,AB平行x 轴,点C在 x 轴上,若点A,B分别在正比例函数 y=6x 和 y=kx 的图象上,则 k=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用 1200 元钱按批发价从蔬菜批发市场买了西红柿和豆角共 400 kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.4 | 3.2 |
零售价(单位:元/kg) | 3.8 | 5.2 |
(1)该经营户所批发的西红柿和豆角的质量分别为多少 kg?
(2)如果西红柿和豆角全部以零售价售出,他当天卖出这些西红柿和豆角赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
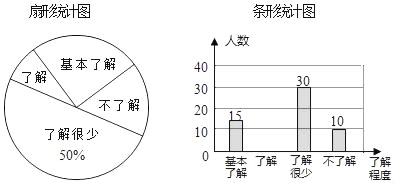
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 °;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
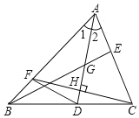
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法:
①D是BC的中点;
②BE⊥AC;
③∠CDA>∠2;
④△AFC为等腰三角形;
⑤连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
其中正确的是________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com