
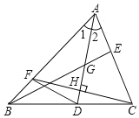
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法:
①D是BC的中点;
②BE⊥AC;
③∠CDA>∠2;
④△AFC为等腰三角形;
⑤连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
其中正确的是________(填序号).
【答案】③④⑤
【解析】
①中依据已知条件无法判断BD=DC,可判断结论错误;
②若BE⊥AC,则∠BAE+∠ABE=90°,结合已知条件可判断;
③根据三角形外角的性质可判断;
④证明△AHF≌△AHC,即可判断;
⑤四边形ACDF的面积等于△AFC的面积与△DFC的面积之和,据此可判断.
解:①根据已知条件无法判断BD=DC,所以无法判断D是BC的中点,故错误;
②只有∠BAE和∠BAC互余时才成立,故错误;
③正确.∵∠ADC=∠1+∠ABD,∠1=∠2,
∴∠ADC>∠2,故②正确;
④正确.∵∠1=∠2,AH=AH,∠AHF=∠AHC=90°,
∴△AHF≌△AHC(ASA),
∴AF=AC,△AFC为等腰三角形,故④正确;
⑤正确.∵AD⊥CF,
![]() .
.
故答案为:③④⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC,BD相交于点O,AC=6,BD=8,∠AOD=65°,点E在BO上,AF∥CE交BD于点F.
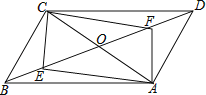
(1)求证:四边形AFCE是平行四边形.
(2)当点E在边BO上移动时,平行四边形AFCE能否为矩形?若能,此时BE的长为多少(直接写出结果)?若不能,请说明理由.
(3)当点E在边BO上移动时,平行四边形AFCE能否为菱形?若能,此时BE的长为多少(直接写出结果)?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等腰三角形ABC,∠A=130°,求∠B的度数
(2)在等腰三角形ABC中,∠A=40°,求∠B的度数.
(3)根据(1)(2)问后发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围,并用含x的式子表示∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(0,a)、B(b+1,0),且a、b满足a2-12a+![]() +36=0,
+36=0,
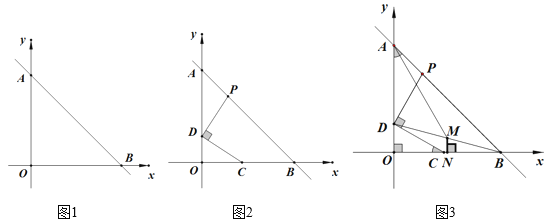
(1)求A、B两点的坐标;
(2)点C在线段BO上(C不与端点B、O重合),点D在线段AO上(D不与端点A、O重合),连CD,过D作CD的垂线交AB于P,若BC=2DO,设C点横坐标为t,求P点横坐标(用含t的代数式表示).
(3)在(2)的条件下,连BD, 点N是BO中点,NM⊥BO,交BD于点M,连AM,若BD=PB,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
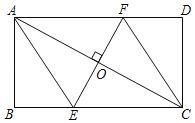
【题目】过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=6,AC=10,EC=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,∠A=∠EDF,再添加一个条件,可使△ABC ≌ △DEF,下列条件不符合的是
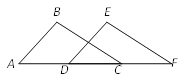
A.∠B=∠EB.BC∥EFC.AD=CFD.AD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,先将正方形纸片对折,折痕为MN,再把点B折叠在折痕MN上,折痕为AE,点E在CB上,点B在MN上的对应点为H,连接DH,则下列选项错误的是( )
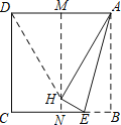
A.△ADH是等边三角形B.NE=![]() BC
BC
C.∠BAE=15°D.∠MAH+∠NEH=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com