
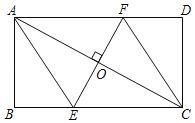
【题目】过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=6,AC=10,EC=![]() ,求EF的长.
,求EF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由矩形的性质可得∠ACB=∠DAC,然后利用“ASA”证明△AOF和△COE全等,根据全等三角形对应边相等可得OE=OF,即可证四边形AECF是菱形;
(2)由菱形的性质可得:菱形AECF的面积=EC×AB=![]() AC×EF,进而得到EF的长.
AC×EF,进而得到EF的长.
解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ACB=∠DAC,
∵O是AC的中点,
∴AO=CO,
在△AOF和△COE中,
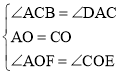 ,
,
∴△AOF≌△COE(ASA),
∴OE=OF,且AO=CO,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形;
(2)∵菱形AECF的面积=EC×AB=![]() AC×EF,
AC×EF,
又∵AB=6,AC=10,EC=![]() ,
,
∴![]() ×6=
×6=![]() ×10×EF,
×10×EF,
解得EF=![]() .
.


科目:初中数学 来源: 题型:
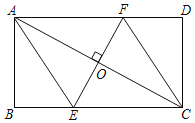
【题目】如图,已知在△ABC中,AB=AC=5,cosB=![]() ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)求△ABC的面积;
(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△APD是直角三角形,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图①由4根火柴棍围成;图②由12根火柴棍围成;图③由24根火柴棍围成;…按此规律,则第⑥个图形由( )根火柴棍围成.
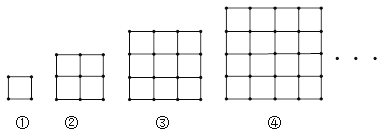
A. 60 B. 72 C. 84 D. 112
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.
(1)求证:E是AD中点;
(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
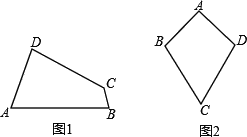
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=78°,∠B=82°,则∠C=_________,∠D=__________
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例(提示:举反例可画图并说明)
(3)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=![]() ,AD=
,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鼎丰超市以固定进价一次性购进保温杯若干个,11月份按一定售价销售,销售额为1800元,为扩大销量,减少库存,12月份在11月份售价基础上打9折销售,结果销售量增加50个,销售额增加630元.
(1)求鼎丰超市11月份这种保温杯的售价是多少元?
(2)如果鼎丰超市11月份销售这种保温杯的利润为600元,那么该鼎丰超市12月份销售这种保温杯的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
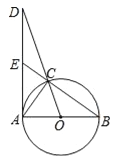
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com