
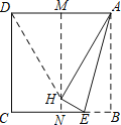
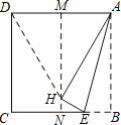
【题目】 如图,先将正方形纸片对折,折痕为MN,再把点B折叠在折痕MN上,折痕为AE,点E在CB上,点B在MN上的对应点为H,连接DH,则下列选项错误的是( )
A.△ADH是等边三角形B.NE=![]() BC
BC
C.∠BAE=15°D.∠MAH+∠NEH=90°
【答案】B
【解析】
依据折叠的性质以及正方形的性质,得到△ADH是等边三角形;依据AM=![]() AD=
AD=![]() AH,得到∠AHM=30°,进而得出∠BAE=15°;依据∠AHE=∠B=90°,∠AMH=∠ENH=90°,即可得到∠MAH+∠NEH=90°.
AH,得到∠AHM=30°,进而得出∠BAE=15°;依据∠AHE=∠B=90°,∠AMH=∠ENH=90°,即可得到∠MAH+∠NEH=90°.
由折叠可得,MN垂直平分AD,AB=AH,
∴DH=AH=AB=AD,
∴△ADH是等边三角形,故A选项正确;
∵BE=HE>NE,
∴BE>![]() BN,
BN,
∴NE=![]() BC不成立,故B选项错误;
BC不成立,故B选项错误;
由折叠可得,AM=![]() AD=
AD=![]() AH,
AH,
∴∠AHM=30°,∠HAM=60°,
又∵∠BAD=90°,
∴∠BAH=30°,
由折叠可得,∠BAE=![]() ∠BAH=15°,故C选项正确;
∠BAH=15°,故C选项正确;
由折叠可得,∠AHE=∠B=90°,
又∵∠AMH=90°,
∴∠AHM+∠HAM=90°,∠AHM+∠EHN=90°,
∴∠HAM=∠EHN,
同理可得∠NEH+∠AHM,
∴∠MAH+∠NEH=90°,故D选项正确;
故选:B.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:初中数学 来源: 题型:
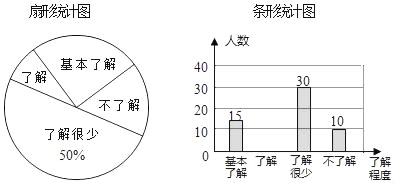
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 °;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
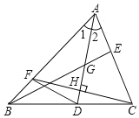
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法:
①D是BC的中点;
②BE⊥AC;
③∠CDA>∠2;
④△AFC为等腰三角形;
⑤连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知:如图1,在Rt△ABC和Rt△A′B′C′中,AB=A′B′,AC=A′C′,∠C=∠C′=90°.求证:Rt△ABC和Rt△A′B′C′全等.
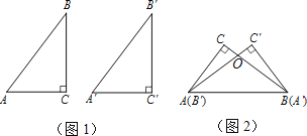
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)如图2,将△ABC和A′B′C′拼在一起(即:点A与点B′重合,点B与点A′重合),BC和B′C′相交于点O,请用此图证明上述命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
科目:初中数学 来源: 题型:
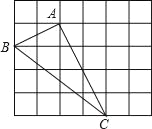
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为_____;
(3)△ACD为 三角形,四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com