
【题目】(1)在等腰三角形ABC,∠A=130°,求∠B的度数
(2)在等腰三角形ABC中,∠A=40°,求∠B的度数.
(3)根据(1)(2)问后发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围,并用含x的式子表示∠B的度数.
【答案】(1)∠B=25°;(2)∠B=70°或100°或40°;(3)当x≠60时,∠B有三个不同的度数,∠B的度数为(![]() )°或(180﹣2x)°或x°.
)°或(180﹣2x)°或x°.
【解析】
(1)根据三角形内角和定理,因为∠A=130°>90°,得到∠B=∠C=25°;
(2)根据三角形内角和定理,因为∠A=40°<90°,所以有∠A=∠B或∠A=∠C或∠B=∠C,分别求出∠B的度数即可;
(3)分两种情况:①当90≤x<180时,∠B的度数只有一个,不符合条件;②当0<x<90时,结合三角形内角和定理先求出三种情况时∠B的度数,再根据∠B的三个度数不同求解即可.
解:(1)根据三角形内角和定理,
∵∠A=130°>90°,
∴∠B=∠C=(180°-130°)÷2=25°;
(2)若∠A为顶角,则∠B=(180°﹣∠A)÷2=70°;
若∠A为底角,∠B为顶角,则∠B=180°﹣2×40°=100°;
若∠A为底角,∠B为底角,则∠B=∠A=40°;
故∠B=70°或100°或40°;
(3)分两种情况:
①当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个,∠B=(![]() )°,不符合条件;
)°,不符合条件;
②当0<x<90时,
若∠A为顶角,则∠B=(![]() )°;
)°;
若∠A为底角,∠B为顶角,则∠B=(180﹣2x)°;
若∠A为底角,∠B为底角,则∠B=x°.
∵∠B有三个不同的同的度数,
∴![]() ≠180﹣2x,180﹣2x≠x或
≠180﹣2x,180﹣2x≠x或![]() ≠x,
≠x,
解得x≠60,
即当x≠60时,∠B有三个不同的度数,∠B的度数为(![]() )°或(180﹣2x)°或x°.
)°或(180﹣2x)°或x°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用 1200 元钱按批发价从蔬菜批发市场买了西红柿和豆角共 400 kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.4 | 3.2 |
零售价(单位:元/kg) | 3.8 | 5.2 |
(1)该经营户所批发的西红柿和豆角的质量分别为多少 kg?
(2)如果西红柿和豆角全部以零售价售出,他当天卖出这些西红柿和豆角赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
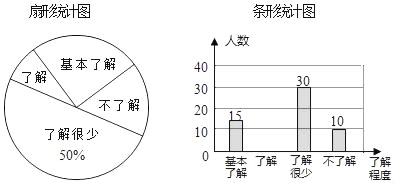
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 °;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
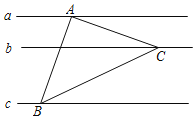
【题目】在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,则△ABC的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
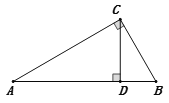
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,△BCD的周长为(6+2![]() )cm,则△ABC的周长为( )cm.
)cm,则△ABC的周长为( )cm.
A.(9+2![]() )B.(12+
)B.(12+![]() )C.(12+4
)C.(12+4![]() )D.(18+2
)D.(18+2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
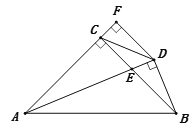
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:① ∠FDC=22.5°; ② 2BD=AE;③ AC+CE=AB; ④ AB-BC=2FC.其中正确的结论有( ) 个
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
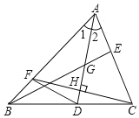
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法:
①D是BC的中点;
②BE⊥AC;
③∠CDA>∠2;
④△AFC为等腰三角形;
⑤连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com