
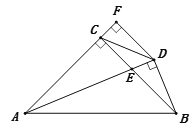
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:① ∠FDC=22.5°; ② 2BD=AE;③ AC+CE=AB; ④ AB-BC=2FC.其中正确的结论有( ) 个
A.1B.2C.3D.4
【答案】D
【解析】
过E作EQ⊥AB于Q,作∠ACN=∠BCD,交AD于N,过D作DH⊥AB于H,根据角平分线性质求出CE=EQ,DM=DH,根据勾股定理求出AC=AQ,AM=AH,根据等腰三角形的性质和判定求出BQ=QE,即可求出③;根据三角形外角性质求出∠CND=45°,证△ACN≌△BCD,推出CD=CN,即可求出①②;证△DCM≌△DBH,得到CM=BH,AM=AH,即可求出④.
解:如图,
∵∠ACB=90°,AE平分∠CAB,
∴CE=EQ,
∵∠ACB=90°,AC=BC,
∴∠CBA=∠CAB=45°,
∵EQ⊥AB,
∴∠EQA=∠EQB=90°,
由勾股定理得:AC=AQ,
∴∠QEB=45°=∠CBA,
∴EQ=BQ,
∴AB=AQ+BQ=AC+CE,
∴③正确;
作∠ACN=∠BCD,交AD于N,
∵∠CAD=![]() ∠CAB=22.5°=∠BAD,
∠CAB=22.5°=∠BAD,
∴∠ABD=90°22.5°=67.5°,
∴∠DBC=67.5°45°=22.5°=∠CAD,
∴∠DBC=∠CAD,
∵AC=BC,∠ACN=∠DCB,
∴△ACN≌△BCD,
∴CN=CD,AN=BD,
∵∠ACN+∠NCE=90°,
∴∠NCB+∠BCD=90°,
∴∠CND=∠CDA=45°,
在![]() 中,∠AFD=90°,∠FCD=22.5°,
中,∠AFD=90°,∠FCD=22.5°,
∴∠FDA=67.5°,
∵∠FDC=∠FDA-∠CDA=22.5°,故①正确;
∴∠ACN=45°22.5°=22.5°=∠CAN,
∴AN=CN,
∴∠NCE=∠AEC=67.5°,
∴CN=NE,
∴CD=AN=EN=![]() AE,
AE,
∵AN=BD,
∴BD=![]() AE,
AE,
故②正确;
过D作DH⊥AB于H,
∵∠MCD=∠CAD+∠CDA=67.5°,
∠DBA=90°∠DAB=67.5°,
∴∠MCD=∠DBA,
∵AE平分∠CAB,DM⊥AC,DH⊥AB,
∴DM=DH,在△DCM和△DBH中∠M=∠DHB=90°,∠FCD=∠DBA,DF=DH,
∴△DCF≌△DBH,
∴BH=CF,由勾股定理得:AF=AH,
∴![]() ,
,
∴AC+AB=2AF,AC+AB=2AC+2CF,ABAC=2CF,
∵AC=CB,
∴ABCB=2CF,
∴④正确;
故答案选:D.


科目:初中数学 来源: 题型:
【题目】2018年3月30日初2018级同学以优异的成绩在双福育才中学完成了中招体育测试,初2019级为了准备明年的体考,对1、2、3、4班进行了体考模拟测试,并对三个班的满分进行了统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
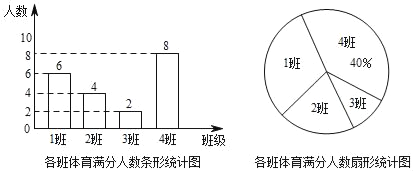
(1)扇形统计图中2班体育成绩满分人数对应的圆心角是 度;并补全条形统计图;
(2)经过体育老师推荐,这些满分同学中有4名同学(1女3男)的跳远动作十分标准,12班班主任准备从这4名同学中任选2名给自己班级的同学示范标准动作,请利用画树状图或列表的方法求出选出2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,A(﹣3,0),B(1,b),则正方形ABCD的面积为( )
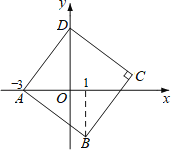
A.34B.25C.20D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在等腰三角形ABC,∠A=130°,求∠B的度数
(2)在等腰三角形ABC中,∠A=40°,求∠B的度数.
(3)根据(1)(2)问后发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围,并用含x的式子表示∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
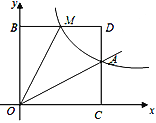
【题目】已知反比例函数![]() 的图象过点A(3,2).
的图象过点A(3,2).
(1)试求该反比例函数的表达式;
(2)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴,交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(0,a)、B(b+1,0),且a、b满足a2-12a+![]() +36=0,
+36=0,
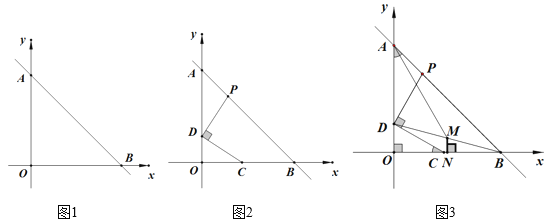
(1)求A、B两点的坐标;
(2)点C在线段BO上(C不与端点B、O重合),点D在线段AO上(D不与端点A、O重合),连CD,过D作CD的垂线交AB于P,若BC=2DO,设C点横坐标为t,求P点横坐标(用含t的代数式表示).
(3)在(2)的条件下,连BD, 点N是BO中点,NM⊥BO,交BD于点M,连AM,若BD=PB,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,∠A=∠EDF,再添加一个条件,可使△ABC ≌ △DEF,下列条件不符合的是
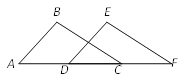
A.∠B=∠EB.BC∥EFC.AD=CFD.AD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
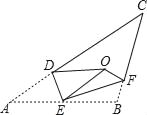
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com