
【题目】如图,平面直角坐标系中,A(0,a)、B(b+1,0),且a、b满足a2-12a+![]() +36=0,
+36=0,
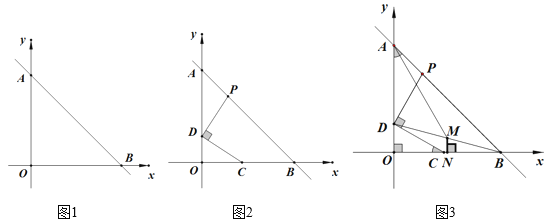
(1)求A、B两点的坐标;
(2)点C在线段BO上(C不与端点B、O重合),点D在线段AO上(D不与端点A、O重合),连CD,过D作CD的垂线交AB于P,若BC=2DO,设C点横坐标为t,求P点横坐标(用含t的代数式表示).
(3)在(2)的条件下,连BD, 点N是BO中点,NM⊥BO,交BD于点M,连AM,若BD=PB,求AM的长.
【答案】(1)A(0,6),B(6,0);(2)点P的横坐标为![]() ;(3)AM=6;
;(3)AM=6;
【解析】
(1)由条件可得![]() ,求出a=6,b=5,则A、B两点的坐标可求;
,求出a=6,b=5,则A、B两点的坐标可求;
(2)过点P作PE⊥0A于点E,证明![]() ,设PE=x,则
,设PE=x,则![]() ,得出方程可求出x=
,得出方程可求出x=![]() ,则P点的橫坐标可求出;
,则P点的橫坐标可求出;
(3)求出直线AB的解析式,由(2)可知点P(![]() ,
,![]() ),由PB=BD可求出
),由PB=BD可求出![]() ,则.M(3,
,则.M(3,![]() ),则AM的长可求出;
),则AM的长可求出;
解:
(1)∵a2-12a+![]() +36=0,
+36=0,
∴![]() ,
,
∴a-6=0,b-5=0,
即a=6,b=5,
∴.A(0,6),B(6,0);
(2)过点P作PE⊥OA于点E,
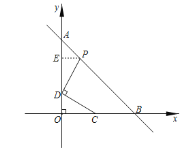
∵C点横坐标为t,BC=2DO,
∴DO=![]() ,
,
∵PD⊥DC,
∴∠PDC=90°,
∴∠PED=∠PDC=∠DOC=90°,
∴∠PDE=∠DCO,
∴![]() ,
,
∴![]() ,
,
设PE=x,则AE=x,DE=![]() ,
,
∴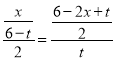 ,
,
∴![]() ,
,
∵t≠-6,
∴![]() ,
,
即点P的横坐标为![]() ;
;
(3)∵A(0,6),B(6,0),
∴设直线AB的解析式为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=-x+6,
由(2)得点P(![]() ,
,![]() ),
),
∵D(0,![]() ),B(6,0),
),B(6,0),
∴![]() ,
,![]() ,
,
∵PB=BD,
∴![]()
![]() ,
,
∴![]() ,
,
解得![]() (负值舍去),
(负值舍去),
∵点N是BO中点,NM⊥BO,
∴M是BD的中点,
∴D(0,![]() ),B(6,0),
),B(6,0),
∴.M(3,![]() ),
),
∴![]() ,
,
∴AM=6;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①是一个重要公式的几何解释.请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B、C、D三点在一条直线上.试证明∠ACE=90°;
(3)伽菲尔德(G a rfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,则△ABC的面积是_____.
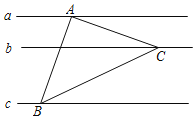
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:① ∠FDC=22.5°; ② 2BD=AE;③ AC+CE=AB; ④ AB-BC=2FC.其中正确的结论有( ) 个
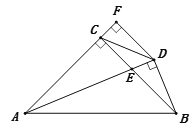
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=∠C,点D在AC上,点E在BC上,AD=CE,BC=DC
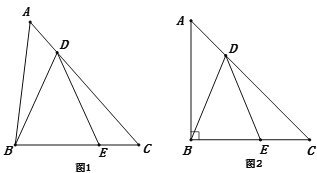
(1)求证:DB=DE;
(2)如图2,若∠ABC=90°,求∠BED的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法:
①D是BC的中点;
②BE⊥AC;
③∠CDA>∠2;
④△AFC为等腰三角形;
⑤连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
其中正确的是________(填序号).
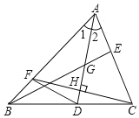
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
关于x的方程:x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() (可变形为x+
(可变形为x+![]() =c+
=c+![]() )的解为x1=c,x2=
)的解为x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Zx+
Zx+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Z.
Z.
(1)归纳结论:根据上述方程与解的特征,得到关于x的方程x+![]() =c+
=c+![]() (m≠0)的解为 .
(m≠0)的解为 .
(2)应用结论:解关于y的方程y﹣a=![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
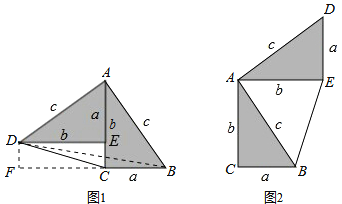
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b-a
S四边形ADCB=![]()
S四边形ADCB=![]()
∴![]() 化简得:a2+b2=c2
化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明,如图(2)中∠DAB=90°,求证:a2+b2=c2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com