
����Ŀ�����ɶ������ض��������֤�����������еġ������������������У�����ϲ�ط��֣�������ȫ�ȵ�ֱ����������ͼ��1���ڷ�ʱ�����������������֤�����ɶ�������������
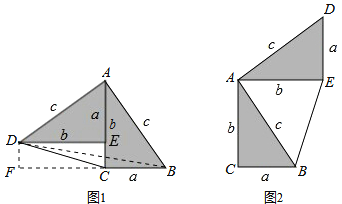
��ͼ��1����DAB=90�㣬��֤��a2+b2=c2
֤��������DB������D��DF��BC��BC���ӳ����ڵ�F����DF=b-a
S�ı���ADCB=![]()
S�ı���ADCB=![]()
��![]() ����ã�a2+b2=c2
����ã�a2+b2=c2
���������֤�������á�������������ͼ��2���Ĺ��ɶ�����֤������ͼ��2���С�DAB=90�㣬��֤��a2+b2=c2

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ��̣�mx2����3m��1��x+2m��2=0��
��1����֤������mȡ��ֵʱ�����̺���ʵ������
��2��������x�Ķ��κ���y=mx2����3m��1��x+2m��2��ͼ����x���������ľ���Ϊ2ʱ���������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�������⣺
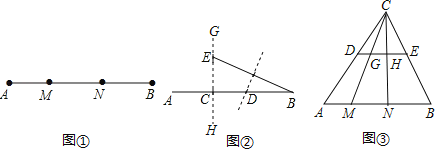
ѧϰ�˹��ɶ���������֪����ֱ������������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ�������ݹ��ɶ������Ƕ��壺��ͼ�٣���M��N���߶�AB�����㣬����߶�AM��MN��NB�ܹ���ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɵ�
�������
��1����ͼ���У����AM��2��MN��3����NB���� ����
��2����ͼ�ڣ���֪��C���߶�AB��һ���㣨AC��BC�������߶�AB������һ��D��ʹ��C��D���߶�AB�Ĺ��ɵ㣮����ͬѧ���������ģ�����C��ֱ��GH��AB����GH�Ͻ�ȡCE��AC������BE����BE�Ĵ�ֱƽ���߽�AB�ڵ�D����C��D���߶�AB�Ĺ��ɵ�����Ϊ����ͬѧ������������˵������
��3����ͼ�ۣ�DE�ǡ�ABC����λ�ߣ�M��N��AB�ߵĹ��ɵ㣨AM��MN��NB��������CM��CN�ֱ�DE�ڵ�G��H��֤��G��H���߶�DE�Ĺ��ɵ㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⱳ������ͼ1�����ı���ABCD�У�AB��AD����BAD��120������B����ADC��90����E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��60������̽��ͼ���߶�BE��EF��FD֮���������ϵ��ʲô��
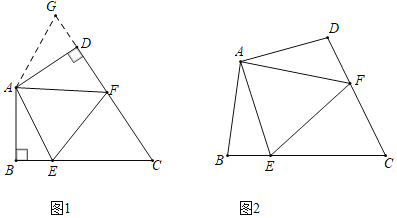
С��̽��������ķ����ǣ��ӳ�FD����G��ʹDG��BE������AG����֤����ABE�ա�ADG����AE��AG�����������ɵá�EAF����GAF��֤����AEF�ա�AGF�������ɵ��߶�BE��EF��FD֮���������ϵ���� ����
��2����չӦ�ã�
��ͼ2�����ı���ABCD�У�AB��AD����B+��D��180����E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��![]() ��BAD���ʣ�1���е��߶�BE��EF��FD֮���������ϵ�Ƿ������������������֤����������������˵�����ɣ�
��BAD���ʣ�1���е��߶�BE��EF��FD֮���������ϵ�Ƿ������������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
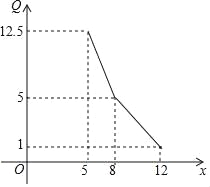
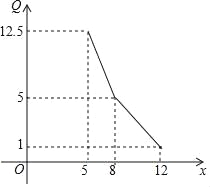
����Ŀ��ijר���꾭�г������֪��һ����Ʒ���������� Q(��λ����)�����ۼ۸� x(��λ����Ԫ/��)�Ĺ�ϵ������ͼ�е����߱�ʾ��
(1)д���������� Q �������ۼ۸� x �Ĺ�ϵ��
(2)�������Ʒ�Ľ���Ϊ 5 ��Ԫ/�֣���ȥ�����ɱ��⣬ר�������۸���Ʒÿ�µĹ̶��ɱ�Ϊ 10 ��Ԫ���ʸ���Ʒ ÿ�ֶ��۶�����Ԫʱ�����۸���Ʒ�����������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����д����֤�������е��������ݣ�
��֪����ͼ��ʾ��AC��BD�ཻ��O��DFƽ����CDO��AC�ཻ��F��BEƽ������ABO��AC�ཻ��E����A����C.��֤����1����2.
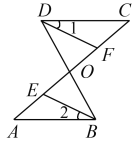
֤�����ߡ�A����C(________)��
��AB��CD (__________________________________)��
���ABO����CDO (__________________________________)��
���ߡ�1��![]() CDO����2��
CDO����2��![]() ��ABO (__________________________________)��
��ABO (__________________________________)��
���1����2(____________________)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijר���꾭�г������֪��һ����Ʒ���������� Q(��λ����)�����ۼ۸� x(��λ����Ԫ/��)�Ĺ�ϵ������ͼ�е����߱�ʾ��
(1)д���������� Q �������ۼ۸� x �Ĺ�ϵ��
(2)�������Ʒ�Ľ���Ϊ 5 ��Ԫ/�֣���ȥ�����ɱ��⣬ר�������۸���Ʒÿ�µĹ̶��ɱ�Ϊ 10 ��Ԫ���ʸ���Ʒ ÿ�ֶ��۶�����Ԫʱ�����۸���Ʒ�����������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
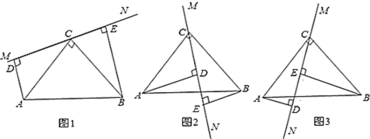
����Ŀ����ͼ1����![]() �У�
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ������Ҫ֤������
������Ҫ֤������
��1����ֱ��![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ2��λ��ʱ�������������䣬����Ϊ���������Ƿ��������������д��֤�����̣�������������д����ʱ
��ת��ͼ2��λ��ʱ�������������䣬����Ϊ���������Ƿ��������������д��֤�����̣�������������д����ʱ![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
��2����ֱ��![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ3��λ��ʱ�������������䣬��ֱ��д����ʱ
��ת��ͼ3��λ��ʱ�������������䣬��ֱ��д����ʱ![]() ֮���������ϵ������Ҫ֤������
֮���������ϵ������Ҫ֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��һ������ε�ÿһ����Ƕ��������ڵ��ڽǵ�![]() �����������1���������ε�ÿһ����ǵĶ�������2�����������ε��ڽǺͣ�
�����������1���������ε�ÿһ����ǵĶ�������2�����������ε��ڽǺͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com