
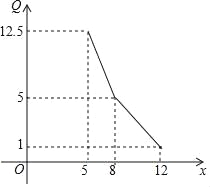
����Ŀ��ijר���꾭�г������֪��һ����Ʒ���������� Q(��λ����)�����ۼ۸� x(��λ����Ԫ/��)�Ĺ�ϵ������ͼ�е����߱�ʾ��
(1)д���������� Q �������ۼ۸� x �Ĺ�ϵ��
(2)�������Ʒ�Ľ���Ϊ 5 ��Ԫ/�֣���ȥ�����ɱ��⣬ר�������۸���Ʒÿ�µĹ̶��ɱ�Ϊ 10 ��Ԫ���ʸ���Ʒ ÿ�ֶ��۶�����Ԫʱ�����۸���Ʒ�����������������������ֵ��
���𰸡���1��Q=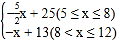 ����2������Ʒÿ�ֶ���9��Ԫʱ�����۸���Ʒ���������������������ֵΪ6��Ԫ
����2������Ʒÿ�ֶ���9��Ԫʱ�����۸���Ʒ���������������������ֵΪ6��Ԫ
��������
��1�����ô���ϵ�����ֱ����ɵã�
��2������������w=Q��x-5��-10���ֱ��5��x��8��8��x��12��������г���������ʽ���䷽�ɶ���ʽ�����ö��κ��������ʿɵã�
��1����5��x��8ʱ����Q=ax+b��
��![]() ����ã�
����ã�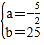 ��
��
��Q=-![]() x+25��
x+25��
ͬ���ɵã���8��x��12ʱ��Q=-x+13��
��Q= ��
��
��2��������w=Q��x-5��-10��
�ɣ�1��֪��w=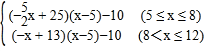 ��
��
��w= ��
��
���Ե�x=9ʱ��wȡ�����ֵ�����ֵΪ6��
�𣺸���Ʒÿ�ֶ���9��Ԫʱ�����۸���Ʒ���������������������ֵΪ6��Ԫ��


 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
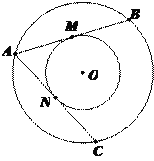
����Ŀ����ͼ����Բ����AB��AC�ֱ���СԲ�ڵ�M��N��
��1����֤��AB=AC��
��2����AB��8����Բ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��![]() x2+bx+c�������ύ��A��B��C���㣬��A�ĺ�����Ϊ��1������C��0��3����ֱ��y=��
x2+bx+c�������ύ��A��B��C���㣬��A�ĺ�����Ϊ��1������C��0��3����ֱ��y=��![]() x+3��x�ύ�ڵ�Q����P���߶�BC�ϵ�һ�����㣬PH��OB�ڵ�H����PB=5t����0��t��1��
x+3��x�ύ�ڵ�Q����P���߶�BC�ϵ�һ�����㣬PH��OB�ڵ�H����PB=5t����0��t��1��
��1��ȷ��b��c��ֵ��
��2��д����B��Q��P�����꣨����Q��P�ú�t��ʽ�ӱ�ʾ����
��3������P�ı仯���Ƿ����t��ֵ��ʹ��PQBΪ���������Σ������ڣ��������t��ֵ���������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɶ������ض��������֤�����������еġ������������������У�����ϲ�ط��֣�������ȫ�ȵ�ֱ����������ͼ��1���ڷ�ʱ�����������������֤�����ɶ�������������
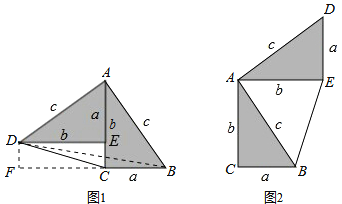
��ͼ��1����DAB=90�㣬��֤��a2+b2=c2
֤��������DB������D��DF��BC��BC���ӳ����ڵ�F����DF=b-a
S�ı���ADCB=![]()
S�ı���ADCB=![]()
��![]() ����ã�a2+b2=c2
����ã�a2+b2=c2
���������֤�������á�������������ͼ��2���Ĺ��ɶ�����֤������ͼ��2���С�DAB=90�㣬��֤��a2+b2=c2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�D��BC�ߵ��е㣬E��AB�ӳ����ϵ�һ�㣬��BE=BD��

��1������BAD����BDE�Ķ�����
��2����֤��AD=DE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90�㣬AB=AC=2����ABΪֱ����Բ��BC��D����ͼ����Ӱ���ֵ����Ϊ��������

A. 1 B. 2 C. 1+![]() D. 2��
D. 2��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
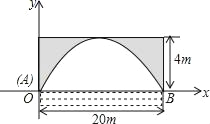
����Ŀ����һ���������ι��ţ�����ˮλʱ����ˮ���Ϊ20m��������ˮ��4m��
��1������ͼ��ֱ������ϵ�У�����������ߵĽ���ʽ��
��2��Ϊ��֤������ֻ˳�����У�����ˮ����Ȳ���С��18m����ˮ��������ˮλ�����ϣ�����Ƕ����ף�����Ӱ�������ֻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
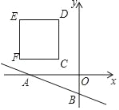
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��![]() x��1�ֱ�x�ᡢy���ڵ�A��B���ڵڶ���������һ�߳�Ϊ2��������CDEF����֪C����1��1����������P��C������ÿ��1����λ���ٶ�����������CDEF�ı���ʱ���˶�һ�ܣ�����C���ֹͣ�˶�������P���˶���ʱ��Ϊt�룮
x��1�ֱ�x�ᡢy���ڵ�A��B���ڵڶ���������һ�߳�Ϊ2��������CDEF����֪C����1��1����������P��C������ÿ��1����λ���ٶ�����������CDEF�ı���ʱ���˶�һ�ܣ�����C���ֹͣ�˶�������P���˶���ʱ��Ϊt�룮
��1���Ƿ����t��ʹ����PΪԲ�ģ�![]() Ϊ�뾶��Բ��ֱ��AB���У������ڣ��������t��ֵ�������ڣ���˵�����ɣ�
Ϊ�뾶��Բ��ֱ��AB���У������ڣ��������t��ֵ�������ڣ���˵�����ɣ�
��2���ڵ�P�˶���ͬʱ��ֱ��AB��ÿ��1����λ���ٶ������������˶������Pͬʱֹͣ���Ƿ����t��ʹ����PΪԲ�ģ�![]() Ϊ�뾶��Բ��ƽ�ƺ��ֱ��A��B�����У���ֱ��д������t��ֵ��
Ϊ�뾶��Բ��ƽ�ƺ��ֱ��A��B�����У���ֱ��д������t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ƽ��ֱ������ϵ����Ҫ��������и�С�⣮
(1)д��ͼ�е�������ABCDEF�������������ϵĵ�����ꣻ
(2)˵����B���C����������ʲô�ص㣿�߶�BC��x����������λ�ù�ϵ��
(3)д����E����y��ĶԳƵ�E�������꣬��ָ����E�����C��������λ�ù�ϵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com