
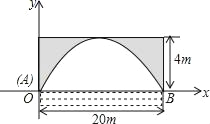
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽为20m,拱顶距水面4m.
(1)在如图的直角坐标系中,求出该抛物线的解析式;
(2)为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水面在正常水位基础上,最多涨多少米,不会影响过往船只?
【答案】(1)y=﹣0.04(x﹣10)2+4(2)0.76m
【解析】
(1)设所求抛物线的解析式为:y=a(x﹣h)2+k,由已知条件易知h和k的值,再把点C的坐标代入求出a的值即可;
(2)由题意得可设E(1,y),把点E的坐标代入已经求出的抛物线解析式求出y的值即可得到最多涨多少米不会影响过往船只.
(1)设所求抛物线的解析式为:y=a(x﹣h)2+k,
∵由AB=20,AB到拱桥顶C的距离为4m,
则C(10,4),A(0,0),B(20,0)
把A,B,C的坐标分别代入得a=﹣0.04,h=10,k=4
抛物线的解析式为y=﹣0.04(x﹣10)2+4;
(2)由题意得可设E(1,y),
把E点坐标代入抛物线的解析式为y=﹣0.04(x﹣10)2+4,
解得:y=﹣0.76,
∴DF=0.76m.


科目:初中数学 来源: 题型:
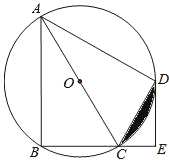
【题目】如图,四边形ABCD是⊙O的内接四边形,![]() ,AC为直径,DE⊥BC,垂足为E.
,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
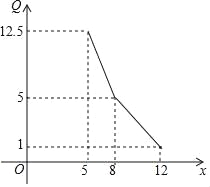
【题目】某专卖店经市场调查得知,一种商品的月销售量 Q(单位:吨)与销售价格 x(单位:万元/吨)的关系可用下图中的折线表示.
(1)写出月销售量 Q 关于销售价格 x 的关系;
(2)如果该商品的进价为 5 万元/吨,除去进货成本外,专卖店销售该商品每月的固定成本为 10 万元,问该商品 每吨定价多少万元时,销售该商品的月利润最大?并求月利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
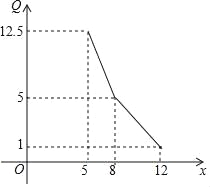
【题目】某专卖店经市场调查得知,一种商品的月销售量 Q(单位:吨)与销售价格 x(单位:万元/吨)的关系可用下图中的折线表示.
(1)写出月销售量 Q 关于销售价格 x 的关系;
(2)如果该商品的进价为 5 万元/吨,除去进货成本外,专卖店销售该商品每月的固定成本为 10 万元,问该商品 每吨定价多少万元时,销售该商品的月利润最大?并求月利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
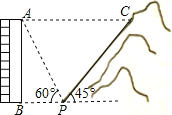
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内。
(1)求居民楼AB的高度;
(2)求C、A之间的距离。(精确到0.1m,参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
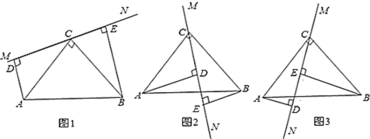
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() .易得
.易得![]() (不需要证明).
(不需要证明).
(1)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时
旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)当直线![]() 绕点
绕点![]() 旋转到图3的位置时,其余条件不变,请直接写出此时
旋转到图3的位置时,其余条件不变,请直接写出此时![]() 之间的数量关系(不需要证明).
之间的数量关系(不需要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
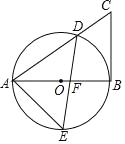
【题目】如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
(1)试判断∠AED与∠C的数量关系,并说明理由;
(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com