
【题目】已知反比例函数![]() 的图象过点A(3,2).
的图象过点A(3,2).
(1)试求该反比例函数的表达式;
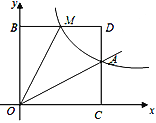
(2)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴,交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.
【答案】(1)![]() ;(2)MB=MD.
;(2)MB=MD.
【解析】
(1)将A(3,2)分别代入y=![]() ,y=ax中,得a、k的值,进而可得正比例函数和反比例函数的表达式;
,y=ax中,得a、k的值,进而可得正比例函数和反比例函数的表达式;
(2)有S△OMB=S△OAC=![]() ×
×![]() =3,可得矩形OBDC的面积为12;即OC×OB=12;进而可得m、n的值,故可得BM与DM的大小;比较可得其大小关系.
=3,可得矩形OBDC的面积为12;即OC×OB=12;进而可得m、n的值,故可得BM与DM的大小;比较可得其大小关系.
(1)将A(3,2)代入![]() 中,得2
中,得2![]() ,∴k=6,
,∴k=6,
∴反比例函数的表达式为![]() .
.
(2)BM=DM,理由:∵S△OMB=S△OAC=![]() ×
×![]() =3,
=3,
∴S矩形OBDC=S四边形OADM+S△OMB+S△OAC=3+3+6=12,
即OC·OB=12,
∵OC=3,∴OB=4,即n=4,∴![]() ,
,
∴MB=![]() ,MD=
,MD=![]() ,∴MB=MD.
,∴MB=MD.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,4),C(8,0).
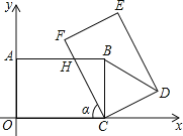
(1)当α=60°时,△CBD的形状是______;
(2)设AH=m
①连接HD,当△CHD的面积等于10时,求m的值;
②当0°<α<90°旋转过程中,连接OH,当△OHC为等腰三角形时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.
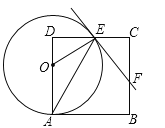
(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,则△ABC的面积是_____.
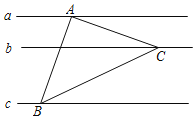
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识背景)我国古代把直角三角形较短的直角边称为“勾”,较长的的直角边称为“股”,斜边称为“弦”.据《周髀算经》记载,公元前1000多年就发现了“勾三股四弦五”的结论.像3、4、5这样为三边长能构成直角三角形的3个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;![]()
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,
当勾为3时,股![]() ,弦
,弦![]() ;
;
当勾为5时,股![]() ,弦
,弦![]() ;
;
当勾为7时,股![]() ,弦
,弦![]() .
.
请仿照上面三组样例,用发现的规律填空:
(1)如果勾用![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股
的式子表示股和弦,则股![]() ,弦
,弦![]() .
.
(问题解决)
(2)古希腊的哲学家柏拉图也提出了构造勾股数组的公式.具体表述如下:如果![]() ,
,![]() ,
,![]() 为大于1的整数),则
为大于1的整数),则![]() 、
、![]() 、
、![]() 为勾股数.请你证明柏拉图公式的正确性;
为勾股数.请你证明柏拉图公式的正确性;
(3)毕达哥拉斯在他找到的勾股数的表达式中发现弦与股的差为1,若用![]() 为任意正整数)表示勾股数中最大的一个数,请你找出另外两个数的表达式分别是多少.
为任意正整数)表示勾股数中最大的一个数,请你找出另外两个数的表达式分别是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:① ∠FDC=22.5°; ② 2BD=AE;③ AC+CE=AB; ④ AB-BC=2FC.其中正确的结论有( ) 个
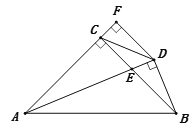
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=∠C,点D在AC上,点E在BC上,AD=CE,BC=DC
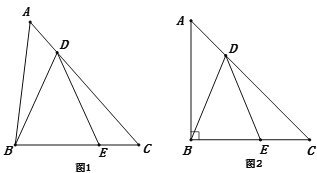
(1)求证:DB=DE;
(2)如图2,若∠ABC=90°,求∠BED的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
关于x的方程:x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() (可变形为x+
(可变形为x+![]() =c+
=c+![]() )的解为x1=c,x2=
)的解为x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Zx+
Zx+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Z.
Z.
(1)归纳结论:根据上述方程与解的特征,得到关于x的方程x+![]() =c+
=c+![]() (m≠0)的解为 .
(m≠0)的解为 .
(2)应用结论:解关于y的方程y﹣a=![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
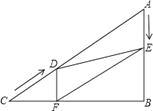
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com