
����Ŀ����ͼ����Rt��ABC�У���B=90����AC=60cm����A=60������D�ӵ�C������CA������4cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루0��t��15��������D��DF��BC�ڵ�F������DE��EF��
��1����֤��AE=DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ����t��ֵ��������ܣ�˵�����ɣ�
��3�����˶������У��ı���BEDF�ܷ�Ϊ�����Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
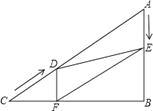
���𰸡���1��֤������������2����t=10ʱ���ı���AEFD�����Σ���3���ı���BEDF����Ϊ�����Σ����ɼ�����.
��������
��1������֪�����ɵ�RT��CDF�С�C=30��������֪DF=![]() CD=AE=2t��
CD=AE=2t��
��2���ɣ�1��֪DF��AE��DF=AE�����ı���ADFE��ƽ���ı��Σ����������Σ����ڱ���ȼ�AD=AE���ɵù���t�ķ��̣���⼴��֪��
��3���ı���BEDF��Ϊ�����Σ������ı����������μ���EDF=90������DE��AB����ʱAD=2AE=4t������AD+CD=AC���t��ֵ���̶��ɵ�DF��BF���ɵô𰸣�
(1)��Rt��ABC��,��B=90��,��A=60����
���C=90����A=30��.
�֡���Rt��CDF��,��C=30����CD=4t
��DF=![]() CD=2t��
CD=2t��
��DF=AE��
(2)��DF��AB��DF=AE��
���ı���AEFD��ƽ���ı��Σ�
��AD=AEʱ���ı���AEFD�����Σ�
��604t=2t����ã�t=10��
����t=10ʱ���ı���AEFD�����Σ�
(3)�ı���BEDF����Ϊ�����Σ��������£�
����EDF=90��ʱ,DE��BC.
���ADE=��C=30��
��AD=2AE
��CD=4t��
��DF=2t=AE��
��AD=4t��
��4t+4t=60��
��t=![]() ʱ,��EDF=90��
ʱ,��EDF=90��
��BF��DF��
���ı���BEDF������Ϊ�����Ρ�


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ��ͼ�����A��3��2����
��ͼ�����A��3��2����
��1������÷����������ı���ʽ��
��2��M��m��n���Ƿ���������ͼ���ϵ�һ���㣬����0��m��3������M��ֱ��MB��x�ᣬ��y���ڵ�B������A��ֱ��AC��y�ᣬ��x���ڵ�C����ֱ��MB�ڵ�D�����ı���OADM�����Ϊ6ʱ�����ж��߶�BM��DM�Ĵ�С��ϵ����˵�����ɣ�
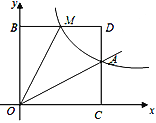
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A(1��0)��B(0��4)��C(4��2)��
��1��������ϵ��������㣨С����������ij���Ϊ��λ1����������ABC�������㼰������Ӻ����أ�
��2������A1B1C1����ABC����y��Գƣ�����ͼ�л�����A1B1C1��
��3����Q��x���ϵ�һ���㣬��ʹQB+QC��С�ĵ�Q����Ϊ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC=15����D�DZ�BC��һ���㣨����B��C�غϣ�����ADE=��B=����DE��AC�ڵ�E����tan��=![]() �����µĽ��ۣ��� ��ADE����ACD���� ��CD=9ʱ����ACD����DBEȫ�ȣ��� ��BDEΪֱ��������ʱ��BDΪ12��
�����µĽ��ۣ��� ��ADE����ACD���� ��CD=9ʱ����ACD����DBEȫ�ȣ��� ��BDEΪֱ��������ʱ��BDΪ12��![]() ���� 0��BE��
���� 0��BE��![]() ��������ȷ�Ľ�����___________��������ȷ���۵���ţ�
��������ȷ�Ľ�����___________��������ȷ���۵���ţ�
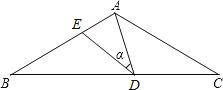
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��DE��EF���ۣ�����A��B�����ڵ�O������EA��EB�غ����߶�EO������CDO+��CFO��100�㣬���C�Ķ���Ϊ��������
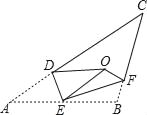
A. 40�� B. 41�� C. 42�� D. 43��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+��2��a��x��2��a��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C���������н��ۣ�
����a��0�������£�����aȡ��ֵ����A��һ�����㣻
����a��0�������£�����aȡ��ֵ�������ߵĶԳ���һ��λ��y�����ࣻ
��y����Сֵ�����ک�2��
����AB=AC����a=![]() ��
��
������ȷ�Ľ����У�����������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������DEFG�Ķ���D��E��![]() �ı�BC�ϣ�����G��F�ֱ��ڱ�AB��AC��
�ı�BC�ϣ�����G��F�ֱ��ڱ�AB��AC��![]() ���
���![]() ��
��![]() �������6����ô��������εı߳���
�������6����ô��������εı߳���![]() ����
����![]()
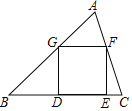
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬
���е㣬![]() �ǶԽ��ߣ�
�ǶԽ��ߣ�![]() ��
��![]() �ӳ�����
�ӳ�����![]() �����ı���
�����ı���![]() �����Σ����ı���
�����Σ����ı���![]() �ǣ� ��
�ǣ� ��
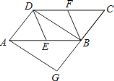
A. ƽ���ı��� B. ����
C. ���� D. ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com