
【题目】如图,![]() ,
,![]() 为
为![]() 内部一条射线,点
内部一条射线,点![]() 为射线
为射线![]() 上一点,
上一点,![]() 为
为![]() ,点
,点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 上的动点,则
上的动点,则![]() 周长的最小值是( )
周长的最小值是( )
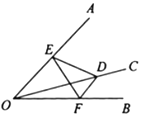
A.![]() B.2C.
B.2C.![]() D.4
D.4
【答案】B
【解析】
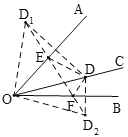
如图,分别作点D关于OA、OB的对称点D1、D2,连接D1D2,交OA于E,OB于F,连接OD1、OD2,根据轴对称的性质可得∠EOD1=∠EOD,∠FOD=∠FOD2,ED1=ED,FD2=FD,OD1=OD=OD2,可得ED1+EF+FD2=DE+EF+DF= D1D2,可知D1D2为△DEF周长的最小值,根据∠AOB=45°可得∠D1OD2=2∠AOB=90°,根据根据勾股定理求出D1D2的长即可得答案.
如图,分别作点D关于OA、OB的对称点D1、D2,连接D1D2,交OA于E,OB于F,连接OD1、OD2,
∴∠EOD1=∠EOD,∠FOD=∠FOD2,ED1=ED,FD2=FD,OD1=OD=OD2,
∴ED1+EF+FD2=DE+EF+DF= D1D2,即D1D2为△DEF周长的最小值,
∵∠EOD1=∠EOD,∠FOD=∠FOD2,∠AOB=45°,∠AOB=∠EOD+∠FOD,
∴∠D1OD2=2∠AOB=90°,
∵OD=![]() ,
,
∴OD1=OD=OD2=![]() ,
,
∴D1D2=![]() =2.
=2.
故选:B.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
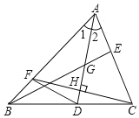
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法:
①D是BC的中点;
②BE⊥AC;
③∠CDA>∠2;
④△AFC为等腰三角形;
⑤连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
科目:初中数学 来源: 题型:
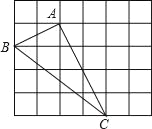
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为_____;
(3)△ACD为 三角形,四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
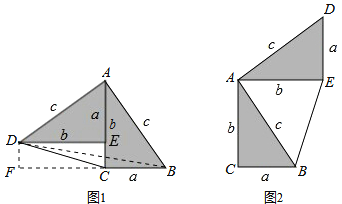
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b-a
S四边形ADCB=![]()
S四边形ADCB=![]()
∴![]() 化简得:a2+b2=c2
化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明,如图(2)中∠DAB=90°,求证:a2+b2=c2
查看答案和解析>>
科目:初中数学 来源: 题型:
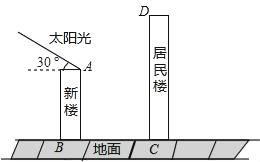
【题目】某住宅小区有一栋面朝正南的居民楼(如图),该居民楼的一楼高为6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.已知冬季正午的阳光与水平线的夹角为30°时.
(1)新楼的建造对超市以上的居民住房冬季正午的采光是否有影响,为什么?
(2)若要使超市冬季正午的采光不受影响,新楼应建在相距居民楼至少多少米的地方,为什么?(结果保留整数,参考数据:sin30°≈0.5,cos30°≈0.87,tan30°≈0.58)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
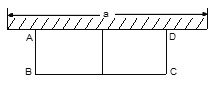
【题目】如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成中间隔有一道篱笆的长方形花圃。
①如果要围成面积为45平方米的花圃,AB的长是多少米?
②能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com