
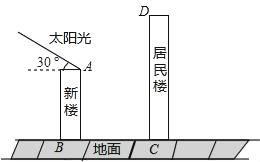
【题目】某住宅小区有一栋面朝正南的居民楼(如图),该居民楼的一楼高为6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.已知冬季正午的阳光与水平线的夹角为30°时.
(1)新楼的建造对超市以上的居民住房冬季正午的采光是否有影响,为什么?
(2)若要使超市冬季正午的采光不受影响,新楼应建在相距居民楼至少多少米的地方,为什么?(结果保留整数,参考数据:sin30°≈0.5,cos30°≈0.87,tan30°≈0.58)
【答案】(1)超市以上的居民住房采光要受影响(2)34米
【解析】
(1)利用三角函数算出阳光可能照到居民楼的什么高度,和6米进行比较.
(2)超市不受影响,说明30°的阳光应照射到楼的底部,根据新楼的高度和30°的正切值即可计算.
解:(1)如图1所示:
过F点作FE⊥AB于点E,
∵EF=15米,∠AFE=30°,
∴AE=5![]() 米,
米,
∴EB=FC=(20﹣5![]() )≈11.34米.
)≈11.34米.
∵11.34>6,
∴超市以上的居民住房采光要受影响;
(2)如图2所示:若要使超市采光不受影响,则太阳光从A直射到C处.
∵AB=20米,∠ACB=30°
∴BC=![]() =20
=20![]() ≈34米
≈34米
答:若要使超市采光不受影响,两楼最少应相距34米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,∠A=∠EDF,再添加一个条件,可使△ABC ≌ △DEF,下列条件不符合的是
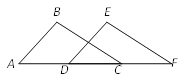
A.∠B=∠EB.BC∥EFC.AD=CFD.AD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
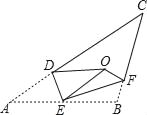
A. 40° B. 41° C. 42° D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
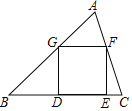
【题目】如图,已知正方形DEFG的顶点D、E在![]() 的边BC上,顶点G、F分别在边AB、AC上
的边BC上,顶点G、F分别在边AB、AC上![]() 如果
如果![]() ,
,![]() 的面积是6,那么这个正方形的边长是
的面积是6,那么这个正方形的边长是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.
(1)求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该商品每天的销售利润最大;
(3)商场的营销部在调控价格方面,提出了A,B两种营销方案.
方案A:每件商品涨价不超过5元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=![]() ,CD=2
,CD=2![]() ,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2
,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2![]() ;④AE=
;④AE=![]() .其中正确的结论是( )
.其中正确的结论是( )
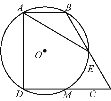
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com