
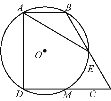
【题目】如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=![]() ,CD=2
,CD=2![]() ,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2
,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2![]() ;④AE=
;④AE=![]() .其中正确的结论是( )
.其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】B
【解析】
连接BD,BM,AM,EM,DE,利用三个角为直角的四边形为矩形得到ABMD为矩形,利用矩形的对边相等得到AB=DM,进而可证明DM=CM,故选项①正确;在Rt△DEC中,由M为CD的中点,利用斜边上的中线等于斜边的一半得到DM与EM相等,从而AB=EM,所以弧AB=弧EM,故选项②正确;先证明四边形AMCB为平行四边形,可得出AM=BC,等量代换得到BC=BD,由BD为圆的直径,可得△DEC为直角三角形,利用勾股定理可求出DE的长,设BE=x,则BD=BC=BE+EC=x+2,在Rt△BDE中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BC的长,即为BD的长,确定出圆的直径,即可对于选项③作出判断;在Rt△AEM中,由AM与ME的长,利用勾股定理求出AE的长,即可对于选项④作出判断.
连接BD,BM,AM,EM,DE,
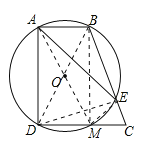
∵∠BAD=90°,
∴BD为圆的直径,
∴∠BMD=90°,
∴∠BAD=∠CDA=∠BMD=90°,
∴四边形ABMD矩形,
∴AB=DM,
又∵CD=2AB,
∴CD=2DM,即DM=MC;
故选项①正确;
在Rt△DEC中,M是DC中点,
∴EM=DM=![]() CD=
CD=![]() ,
,
∴弧EM=弧DM,
又∵AB=DM,
∴弧AB=弧DM,
∴弧AB=弧EM,
故选项②正确;
∵AB∥MC,AB=MC,
∴四边形ABCM是平行四边形,
∴AM=BC,又BD=AM,
∴BD=BC,
∵BD是直径,
∴∠BED=90°,即∠DEC=90°,
又EC=2,DC=2![]() ,
,
根据勾股定理得:DE=![]() =2
=2![]() ,
,
设BE=x,BD=BC=BE+EC=x+2,
在Rt△BDE中,根据勾股定理得:BE2+DE2=BD2,即x2+20=(x+2)2,
解得:x=4,
∴BD=6,故选项③错误;
在Rt△AEM中,AM=6,EM=![]() ,
,
根据勾股定理得:AE=![]() =
=![]() ;
;
故选项④正确;
则正确的选项为:①②④.
故选B.


科目:初中数学 来源: 题型:
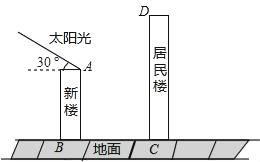
【题目】某住宅小区有一栋面朝正南的居民楼(如图),该居民楼的一楼高为6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.已知冬季正午的阳光与水平线的夹角为30°时.
(1)新楼的建造对超市以上的居民住房冬季正午的采光是否有影响,为什么?
(2)若要使超市冬季正午的采光不受影响,新楼应建在相距居民楼至少多少米的地方,为什么?(结果保留整数,参考数据:sin30°≈0.5,cos30°≈0.87,tan30°≈0.58)
查看答案和解析>>
科目:初中数学 来源: 题型:
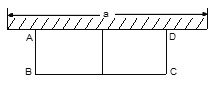
【题目】如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成中间隔有一道篱笆的长方形花圃。
①如果要围成面积为45平方米的花圃,AB的长是多少米?
②能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
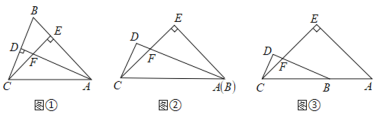
【题目】如图①,已知![]() 是等腰三角形,
是等腰三角形,![]() 是
是![]() 边上的高,垂足为
边上的高,垂足为![]() ,
,![]() 是底边
是底边![]() 上的高,交
上的高,交![]() 于点
于点![]() .
.
(1)若![]() .求证:
.求证:![]() ≌
≌![]() ;
;
(2)在图②, 图③中,![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 在线段
在线段![]() 上(不含点
上(不含点![]() ),
),![]() ,且
,且![]() 交
交![]() 于点
于点![]() ,
,![]() ,垂足为
,垂足为![]() .
.
ⅰ)如图②,当点![]() 与点
与点![]() 重合,试写出
重合,试写出![]() 与
与![]() 的数量关系;
的数量关系;
ⅱ)如图③,当点![]() 在线段
在线段![]() 上(不含点
上(不含点![]() ,
,![]() )时,ⅰ)中的结论成立吗?如果成立,请证明;如果不成立,请说明理由.
)时,ⅰ)中的结论成立吗?如果成立,请证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() :
: ![]() 与抛物线
与抛物线![]() 相交于点A(
相交于点A(![]() ,7).
,7).
(1)求m,n的值;
(2)过点A作AB∥x轴交抛物线于点B,设抛物线与x轴交于点C、D(点C在点D的左侧),求△BCD的面积;
(3)点E(t,0)为x轴上一个动点,过点E作平行于y轴的直线与直线![]() 和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.
和抛物线分别交于点P、Q.当点P在点Q上方时,求线段PQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数![]() (利润=售价﹣制造成本).
(利润=售价﹣制造成本).
(1)写出每月的利润w(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?
(3)当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
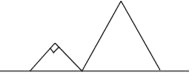
【题目】如图,直角边长为![]() 的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
A. 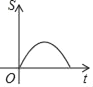 B.
B. 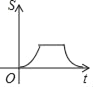
C. 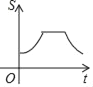 D.
D. 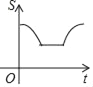
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com