
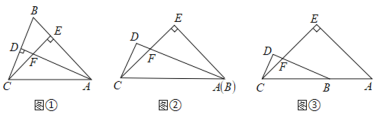
【题目】如图①,已知![]() 是等腰三角形,
是等腰三角形,![]() 是
是![]() 边上的高,垂足为
边上的高,垂足为![]() ,
,![]() 是底边
是底边![]() 上的高,交
上的高,交![]() 于点
于点![]() .
.
(1)若![]() .求证:
.求证:![]() ≌
≌![]() ;
;
(2)在图②, 图③中,![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 在线段
在线段![]() 上(不含点
上(不含点![]() ),
),![]() ,且
,且![]() 交
交![]() 于点
于点![]() ,
,![]() ,垂足为
,垂足为![]() .
.
ⅰ)如图②,当点![]() 与点
与点![]() 重合,试写出
重合,试写出![]() 与
与![]() 的数量关系;
的数量关系;
ⅱ)如图③,当点![]() 在线段
在线段![]() 上(不含点
上(不含点![]() ,
,![]() )时,ⅰ)中的结论成立吗?如果成立,请证明;如果不成立,请说明理由.
)时,ⅰ)中的结论成立吗?如果成立,请证明;如果不成立,请说明理由.
【答案】(1)见解析;(2)ⅰ)![]() ;ⅱ)成立,证明见解析
;ⅱ)成立,证明见解析
【解析】
(1)如图1,根据同角的余角相等证明![]() ,利用ASA证明
,利用ASA证明![]() ≌
≌![]() ;
;
(2)①如图2,作辅助线,构建全等三角形,证明![]() ≌
≌![]() ,则CP=AF,再证明
,则CP=AF,再证明![]() ≌
≌![]() ,可得结论;
,可得结论;
②结论仍然成立,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,且于
,且于![]() 的延长线相交于点
的延长线相交于点![]() ,证明
,证明![]() ≌
≌![]() ,得
,得![]() ,再证明
,再证明![]() ≌
≌![]() 即可求解.
即可求解.
证明:(1)∵![]()
∴![]()
∵![]()
∴![]()
在![]() 和
和![]() 中
中
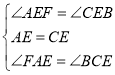
∴![]() ≌
≌![]() ;
;
(2)ⅰ):![]()
证明过程如下:延长![]() 、
、![]() 交于点
交于点![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴AE=CE,
又![]()
∴![]() ≌
≌![]()
∴![]()
∵![]()
∴![]() 平分
平分![]()
则![]()
∵![]()
∴![]()
又AD=AD
∴![]() ≌
≌![]() (ASA)
(ASA)
∴![]()
∴![]()
∴![]() ;
;
ⅱ)成立,即![]()
证明如下:过点![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,且于
,且于![]() 的延长线相交于点
的延长线相交于点![]()
∴![]() ,
,
∴![]() =
=![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴CQ=QB
同理可得![]() ≌
≌![]()
∴![]()
∵![]() =
=![]()
∴BD平分![]()
则![]()
∵![]()
∴![]() =90
=90![]()
又BD=BD
∴![]() ≌
≌![]() (ASA)
(ASA)
∴![]()
∴![]()
∴![]() .
.


科目:初中数学 来源: 题型:
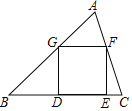
【题目】如图,已知正方形DEFG的顶点D、E在![]() 的边BC上,顶点G、F分别在边AB、AC上
的边BC上,顶点G、F分别在边AB、AC上![]() 如果
如果![]() ,
,![]() 的面积是6,那么这个正方形的边长是
的面积是6,那么这个正方形的边长是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 延长线于
延长线于![]() .若四边形
.若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 是( )
是( )
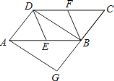
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晨光文具店有一套体育用品:1个篮球,1个排球和1个足球,一套售价300元,也可以单独出售,小攀同学共有50元、20元、10元三种面额钞票各若干张.如果单独出售,每个球只能用到同一种面额的钞票去购买.若小面额的钱的张数恰等于另两种面额钱张数的乘积,那么所有可能中单独购买三个球中所用到的钱最少的一个球是___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 是矩形,
是矩形,![]() ,
,![]() 。动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,Q以2cm/s的速度向B移动.
。动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,Q以2cm/s的速度向B移动.
(1)P、Q两点从出发开始几秒后,四边形ABQP的面积是矩形面积的![]() ?
?
(2)P、Q从开始出发几秒后,![]() ?
?
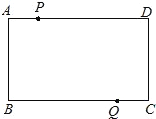
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=![]() ,CD=2
,CD=2![]() ,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2
,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2![]() ;④AE=
;④AE=![]() .其中正确的结论是( )
.其中正确的结论是( )
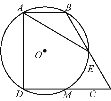
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:

(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列例题的解答过程:解方程:3(x﹣2)2+7(x﹣2)+4=0.
解:设 x﹣2=y,则原方程化为:3y2+7y+4=0.
∵a=3,b=7,c=4,∴b2﹣4ac=72﹣4×3×4=1.
∴y=![]() =
=![]() .∴y1=﹣1,y2=﹣
.∴y1=﹣1,y2=﹣![]() .
.
当 y=﹣1 时,x﹣2=﹣1,∴x=1;
当 y=﹣![]() 时,x﹣2=﹣
时,x﹣2=﹣![]() ,∴x=
,∴x=![]() .
.
∴原方程的解为:x1=1,x2=![]() .
.
(1)请仿照上面的例题解一元二次方程:2(x﹣3)2﹣5(x﹣3)﹣7=0;
(2)若(a2+b2)(a2+b2﹣2)=3,求代数式 a2+b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=4,∠A=60°,若边AC的垂直平分线DE交AB于点D,连接CD,则△BDC的周长为( )
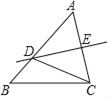
A. 8 B. 9 C. 5+![]() D. 5+
D. 5+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com