
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:

(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.

【答案】(1)这个二次函数的表达式为![]() ;(2)
;(2)![]() ;(3)画图见解析;(4)x<-3或x>1.
;(3)画图见解析;(4)x<-3或x>1.
【解析】试题分析:
(1)观察表格中的数据可知,该抛物线的顶点坐标为(-1,2),因此可设其解析式为顶点式: ![]() ,再代入表格除顶点外的一对对应值,求出a的值即可得到抛物线的解析式;
,再代入表格除顶点外的一对对应值,求出a的值即可得到抛物线的解析式;
(2)根据抛物线的对称性,结合表格可知,当![]() 时的函数值是相等的,由此可得m=
时的函数值是相等的,由此可得m=![]() ;
;
(3)根据表格中的数据可知,该抛物线的对称轴为直线: ![]() ,顶点坐标为(-1,2),与
,顶点坐标为(-1,2),与![]() 相交于点(-3,0)和点(1,0),由此通过描点、连线即画出该抛物线的图象;
相交于点(-3,0)和点(1,0),由此通过描点、连线即画出该抛物线的图象;
(4)观察图象找到抛物线在![]() 轴下方部分图象所对应的自变量的取值范围即可得到答案.
轴下方部分图象所对应的自变量的取值范围即可得到答案.
试题解析:
(1)观察表格中的数据可知,该抛物线的顶点坐标为(-1,2),
∴可设这个二次函数的表达式为![]() ,
,
又∵图象过点(1,0),
∴![]() ,解得
,解得![]() ,
,
∴这个二次函数的表达式为![]() ;
;
(2)∵该抛物线的对称轴为直线: ![]() ,
,
∴当![]() 时的函数值是相等的,
时的函数值是相等的,
∴由表格中的数据可知:m=![]() ;
;
(3)根据表格中的数据可知,该抛物线的对称轴为直线: ![]() ,顶点坐标为(-1,2),与
,顶点坐标为(-1,2),与![]() 相交于点(-3,0)和点(1,0),由此通过描点、连线可得该抛物线的图象如下图所示:
相交于点(-3,0)和点(1,0),由此通过描点、连线可得该抛物线的图象如下图所示:
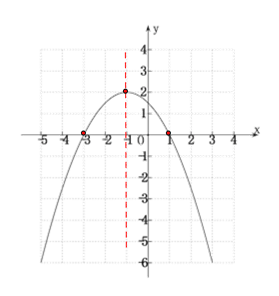
(4)观察图象可得:当![]() 时,
时, ![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解的过程:
解:设a2-4a=y,则
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(a2-4a+4)2.(第四步)
(1)该同学因式分解的结果是否彻底:________(填“彻底”或“不彻底”);
(2)若不彻底,请你直接写出因式分解的最后结果:________;
(3)请你模仿以上方法对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技实践社团制作实践设备,小明的操作过程如下:
①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;
②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);
③用一细橡胶棒连接C、D两点(如图3);
④计算出橡胶棒CD的长度.
小明计算橡胶棒CD的长度为( )

A. 2![]() 分米 B. 2
分米 B. 2![]() 分米 C. 3
分米 C. 3![]() 分米 D. 3
分米 D. 3![]() 分米
分米
查看答案和解析>>
科目:初中数学 来源: 题型:
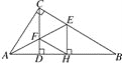
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
求证:(1)CF=CE
(2)四边形CFHE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生自主意识,拓宽学生视野,促进学习与生活的深度融合我市某中学决定组织部分学生去青少年综合实践基地进行综合实践活动在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生现有甲、乙两种大客车它们的载客量和租金如表所示
甲种客车 | 乙种客车 | |
载客量(人/辆) | 30 | 42 |
租金(元/辆) | 300 | 400 |
学校计划此实践活动的租车总费用不超过3100元,为了安全每辆客车上至少要有2名老师.
(1)参加此次综合实践活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,租用客车总数为多少辆?
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮相约晨练跑步,小明比小亮早1分钟离开家门,3分钟后迎面遇到从家跑来的小亮,两人沿滨江路跑了2分钟后,决定进行长跑比赛,比赛时小明的速度始终是180米/分,小亮的速度始终是220米/分.如图是两人之间的距离y(米)与小明离开家的时间x(分)之间的函数图象,则下列结论中正确的是____________________.(写序号即可)
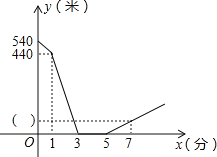
①小明家与小亮家距离为540米;
②小亮比赛前的速度为120米/分;
③小明出发7分钟时,两人距离为80米;
④若小亮从家出门跑了14分钟后,按原路以比赛时的速度返回,则再经过1分钟两人相遇.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com