
ЁОЬтФПЁПФГаЃПЦММЪЕМљЩчЭХжЦзїЪЕМљЩшБИЃЌаЁУїЕФВйзїЙ§ГЬШчЯТЃК
ЂйаЁУїШЁГіРЯЪІЬсЙЉЕФдВаЮЯИЬњЛЗЃЌЯШЭЈЙ§дкдВвЛеТжабЇЕНЕФжЊЪЖевЕНдВаФOЃЌдйШЮвтевГідВOЕФвЛЬѕжБОЖБъМЧЮЊABЃЈШчЭМ1ЃЉЃЌВтСПГіAB=4ЗжУзЃЛ
ЂкНЋдВЛЗНјааЗелЪЙЕуBТфдкдВаФOЕФЮЛжУЃЌЗелВПЗжЕФдВЛЗКЭЮДЗелЕФдВЛЗВњЩњНЛЕуЗжБ№БъМЧЮЊCЁЂDЃЈШчЭМ2ЃЉЃЛ
ЂлгУвЛЯИЯ№НКАєСЌНгCЁЂDСНЕуЃЈШчЭМ3ЃЉЃЛ
ЂмМЦЫуГіЯ№НКАєCDЕФГЄЖШ.
аЁУїМЦЫуЯ№НКАєCDЕФГЄЖШЮЊЃЈ ЃЉ

A. 2![]() ЗжУз B. 2
ЗжУз B. 2![]() ЗжУз C. 3
ЗжУз C. 3![]() ЗжУз D. 3
ЗжУз D. 3![]() ЗжУз
ЗжУз
 бєЙтПМГЁЕЅдЊВтЪдОэЯЕСаД№АИ
бєЙтПМГЁЕЅдЊВтЪдОэЯЕСаД№АИ УћаЃСЊУЫГхДЬОэЯЕСаД№АИ
УћаЃСЊУЫГхДЬОэЯЕСаД№АИ УћаЃЬсЗжвЛОэЭЈЯЕСаД№АИ
УћаЃЬсЗжвЛОэЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊGЁЂHЗжБ№ЪЧЁѕABCDЖдБпADЁЂBCЩЯЕФЕуЃЌжБЯпGHЗжБ№НЛBAКЭDCЕФбгГЄЯпгкЕуEЁЂFЃЎ
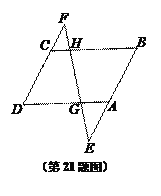
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉСЊНсBDНЛEFгкЕуMЃЌЧѓжЄЃКMGЁЄME=MFЁЄMH.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧгУ![]() БэЪОВЛДѓгк
БэЪОВЛДѓгк![]() ЕФзюДѓећЪ§ЃЌР§ШчЃК
ЕФзюДѓећЪ§ЃЌР§ШчЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛгУ
ЃЛгУ![]() БэЪОДѓгк
БэЪОДѓгк![]() ЕФзюаЁећЪ§ЃЌР§ШчЃК
ЕФзюаЁећЪ§ЃЌР§ШчЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .НтОіЯТСаЮЪЬтЃК
.НтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() = ,ЃЌ
= ,ЃЌ![]() = ЃЛ
= ЃЛ
ЃЈ2ЃЉШє![]() =2ЃЌдђ
=2ЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ ЃЛШє
ЕФШЁжЕЗЖЮЇЪЧ ЃЛШє![]() =Ѓ1ЃЌдђ
=Ѓ1ЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЃЈ3ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ТњзуЗНГЬзщ
ТњзуЗНГЬзщ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЃЌ
ЃЌ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮABCDжаЃЌABЃН3ЃЌADЃН4ЃЌНЋЁїABDбизХBDелЕўЃЌЪЙЕуAгыЕуEжиКЯЃЎ
ЃЈ1ЃЉШчЭМЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌСЌНгOEЃЌдђЯпЖЮOEЕФГЄЃН ЃЛ
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуEзїEFЁЮCDНЛЯпЖЮBDгкЕуFЃЌСЌНгAFЃЌЧѓжЄЃКЫФБпаЮABEFЪЧСтаЮЃЛ
ЃЈ3ЃЉШчЭМЃЌдкЃЈ2ЃЉЬѕМўЯТЃЌЯпЖЮAEЁЂBDЯрНЛгкMЃЌСЌНгCEЃЌЧѓЯпЖЮCEЕФГЄЃЎ
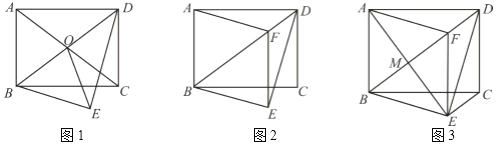
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЕФЖЅЕузјБъЮЊЃКA(1ЃЌ2)ЃЌB(2ЃЌ вЛ1)ЃЌ C (4ЃЌ 3)ЃЎ
(1)НЋЁїABCЯђзѓЦНвЦ2ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЁїAЃЇBЃЇCЃЇЃЎЛГіЁїAЃЇBЃЇCЃЇЃЌВЂаДГіЁїAЃЇBЃЇCЃЇЕФЖЅЕузјБъЃЛ
(2)ЧѓЁїABCЕФУцЛ§ЃЎ
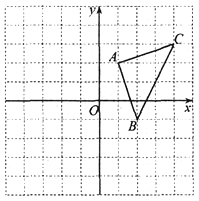
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпAPНЛxжсгкЕуPЃЈpЃЌ0ЃЉЃЌНЛyжсгкЕуAЃЈ0ЃЌaЃЉЃЌЧвaЁЂpТњзу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжБЯпAPЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуPЙигкyжсЕФЖдГЦЕуЮЊQЃЌRЃЈ0ЃЌ2ЃЉЃЌЕуSдкжБЯпAQЩЯЃЌЧвSR=SAЃЌЧѓжБЯпRSЕФНтЮіЪНКЭЕуSЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуBЃЈЉ2ЃЌbЃЉЮЊжБЯпAPЩЯвЛЕуЃЌвдABЮЊаББпзїЕШбќжБНЧШ§НЧаЮABCЃЌЕуCдкЕквЛЯѓЯоЃЌDЮЊЯпЖЮOPЩЯвЛЖЏЕуЃЌСЌНгDCЃЌвдDCЮЊжБНЧБпЃЌЕуDЮЊжБНЧЖЅЕузїЕШбќШ§НЧаЮDCEЃЌEFЁЭxжсЃЌFЮЊДЙзуЃЌЯТСаНсТлЃКЂй2DP+EFЕФжЕВЛБфЃЛЂк![]() ЕФжЕВЛБфЃЛЦфжажЛгавЛИіНсТле§ШЗЃЌЧыФубЁдёГіе§ШЗЕФНсТлЃЌВЂЧѓГіЦфЖЈжЕЃЎ
ЕФжЕВЛБфЃЛЦфжажЛгавЛИіНсТле§ШЗЃЌЧыФубЁдёГіе§ШЗЕФНсТлЃЌВЂЧѓГіЦфЖЈжЕЃЎ
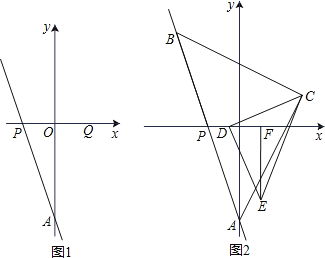
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіЖўДЮКЏЪ§ЭМЯѓЩЯВПЗжЕуЕФКсзјБъxЃЌзнзјБъyЕФЖдгІжЕШчЯТБэЃК

(1)ЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
(2)ЧѓmЕФжЕЃЛ
(3)дкИјЖЈЕФжБНЧзјБъЯЕжаЃЌЛГіетИіКЏЪ§ЕФЭМЯѓЃЛ
(4)ИљОнЭМЯѓЃЌаДГіЕБyЃМ0ЪБЃЌxЕФШЁжЕЗЖЮЇ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=BC=4ЃЌAO=BOЃЌPЪЧЩфЯпCOЩЯЕФвЛИіЖЏЕуЃЌЁЯAOC=60ЁуЃЌдђЕБЁїPABЮЊжБНЧШ§НЧаЮЪБЃЌAPЕФГЄЮЊ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
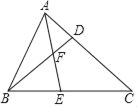
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуDЁЂEЗжБ№дкЁїABCЕФБпACЁЂBCЩЯЃЌЯпЖЮBDгыAEНЛгкЕуFЃЌЧвCDCA=CECBЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯCAE=ЁЯCBDЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓжЄЃКABAD=AFAEЃЎ
ЃЌЧѓжЄЃКABAD=AFAEЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com