
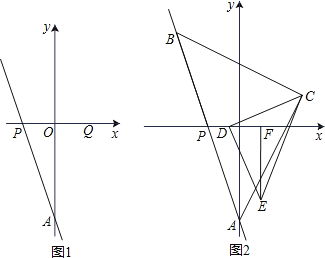
【题目】如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、p满足![]() .
.
(1)求直线AP的解析式;
(2)如图1,点P关于y轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;
(3)如图2,点B(﹣2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②![]() 的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
【答案】(1)y=﹣3x﹣3;(2)S(![]() ,﹣
,﹣![]() ), y=﹣3x+2;(3)②;定值为
), y=﹣3x+2;(3)②;定值为![]() .
.
【解析】
(1)根据非负数的性质列式求出a、p的值,从而得到点A、P的坐标,然后利用待定系数法求直线的解析式;
(2)根据关于y轴的点的对称求出点Q的坐标,再利用待定系数法求出直线AQ的解析式,设出点S的坐标,然后利用两点间的距离公式列式进行计算即可求出点S的坐标,再利用待定系数法求解直线RS的解析式;
(3)根据点B的横坐标为-2,可知点P为AB的中点,然后求出点B得到坐标,连接PC,过点C作CG⊥x轴于点G,利用角角边证明△APO与△PCG全等,根据全等三角形对应边相等可得PG=AO,CG=PO,再根据△DCE是等腰直角三角形,利用角角边证明△CDG与△EDF全等,根据全等三角形对应边相等可得DG=EF,然后用EF表示出DP的长度,然后代入两个结论进行计算即可找出正确的结论并得到定值.
(1)根据题意得,a+3=0,p+1=0,
解得a=﹣3,p=﹣1,
∴点A、P的坐标分别为A(0,﹣3)、P(﹣1,0),
设直线AP的解析式为y=mx+n,
则![]() ,
,
解得![]() ,
,
∴直线AP的解析式为y=﹣3x﹣3;
(2)根据题意,点Q的坐标为(1,0),
设直线AQ的解析式为y=kx+c,
则![]() ,
,
解得![]() ,
,
∴直线AQ的解析式为y=3x﹣3,
设点S的坐标为(x,3x﹣3),
则SR=![]() ,
,
SA=![]() ,
,
∵SR=SA,
∴![]() =
=![]() ,
,
解得x=![]() ,
,
∴3x﹣3=3×![]() ﹣3=﹣
﹣3=﹣![]() ,
,
∴点S的坐标为S(![]() ,﹣
,﹣![]() ),
),
设直线RS的解析式为y=ex+f,
则 ,
,
解得![]() ,
,
∴直线RS的解析式为y=﹣3x+2;
(3)∵点B(﹣2,b),
∴点P为AB的中点,
连接PC,过点C作CG⊥x轴于点G,
∵△ABC是等腰直角三角形,
∴PC=PA=![]() AB,PC⊥AP,
AB,PC⊥AP,
∴∠CPG+∠APO=90°,∠APO+∠PAO=90°,
∴∠CPG=∠PAO,
在△APO与△PCG中,
 ,
,
∴△APO≌△PCG(AAS),
∴PG=AO=3,CG=PO,
∵△DCE是等腰直角三角形,
∴CD=DE,∠CDG+∠EDF=90°,
又∵EF⊥x轴,
∴∠DEF+∠EDF=90°,
∴∠CDG=∠DEF,
在△CDG与△EDF中,
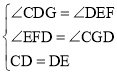 ,
,
∴△CDG≌△EDF(AAS),
∴DG=EF,
∴DP=PG﹣DG=3﹣EF,
①2DP+EF=2(3﹣EF)+EF=6﹣EF,
∴2DP+EF的值随点D的变化而变化,不是定值,
②![]() ,
,
![]() 的值与点D的变化无关,是定值
的值与点D的变化无关,是定值![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法:①若|a|=-b,|b|=b,则a=b=0;②若-a不是正数,则a为非负数;③|-a![]() |=(-a)
|=(-a)![]() ; ④若
; ④若![]() ,则
,则![]() ; ⑤若a+b=0,则a3+b3=0; ⑥若|a|>b,则a2>b2;其中正确的结论有( )
; ⑤若a+b=0,则a3+b3=0; ⑥若|a|>b,则a2>b2;其中正确的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人用![]() 元购买了
元购买了![]() 套儿童服装,准备以一定价格出售,如果以每套儿童服装
套儿童服装,准备以一定价格出售,如果以每套儿童服装![]() 元的价格为标准,超出的记作正数,不足的记作负数,记录如下:
元的价格为标准,超出的记作正数,不足的记作负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .(单位:元)
.(单位:元)
(1)最高售价比最低高出多少?
(2)当他卖完这![]() 套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技实践社团制作实践设备,小明的操作过程如下:
①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;
②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);
③用一细橡胶棒连接C、D两点(如图3);
④计算出橡胶棒CD的长度.
小明计算橡胶棒CD的长度为( )

A. 2![]() 分米 B. 2
分米 B. 2![]() 分米 C. 3
分米 C. 3![]() 分米 D. 3
分米 D. 3![]() 分米
分米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 经过某种变换后得到点
经过某种变换后得到点![]() ,我们把点
,我们把点![]() 叫做点
叫做点![]() 的终结点.已知点
的终结点.已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() 、…
、…![]() 、…,若点
、…,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
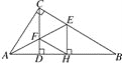
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
求证:(1)CF=CE
(2)四边形CFHE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(2,0),∠ABO=30°,且AB⊥BC.

(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 满足条件:(1)在
满足条件:(1)在![]() 时,
时, ![]() 随
随![]() 的增大而增大,在
的增大而增大,在![]() 时,
时, ![]() 随
随![]() 的增大而减小;(2)与
的增大而减小;(2)与![]() 轴有两个交点,且两个交点间的距离小于
轴有两个交点,且两个交点间的距离小于![]() .以下四个结论:①
.以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,说法正确的个数有( )个
,说法正确的个数有( )个
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com