
【题目】某人用![]() 元购买了
元购买了![]() 套儿童服装,准备以一定价格出售,如果以每套儿童服装
套儿童服装,准备以一定价格出售,如果以每套儿童服装![]() 元的价格为标准,超出的记作正数,不足的记作负数,记录如下:
元的价格为标准,超出的记作正数,不足的记作负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .(单位:元)
.(单位:元)
(1)最高售价比最低高出多少?
(2)当他卖完这![]() 套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
【答案】(1)5元;(2)盈利37元.
【解析】
(1)根据正负数的意义找出最大的数加上55为最高价,最小的数加上55为最低价,即可解答;
(2)以55元为标准记录的8个数字相加,再加上55×8,即可求出8套衣服的总售价,与400元比较,若大于400,则盈利;若小于400,则亏损;若盈利,就用卖衣服的总价钱![]() 就是盈利的钱,若亏损,就用
就是盈利的钱,若亏损,就用![]() 买衣服的总价钱,就是亏损的钱.
买衣服的总价钱,就是亏损的钱.
解:(1)最高售价为:55+2=57元;最低售价为:55+(-3)=52元;
∴最高售价比最低高出的价格=57-52=5元;
答:最高售价比最低高出5元
(2)根据题意得
![]() ,
,
![]() 元,
元,
![]() ,
,![]() 元,
元,
故盈利37元.
答:当他卖完这![]() 套儿童服装后是盈利,盈利了37元钱.
套儿童服装后是盈利,盈利了37元钱.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,a是
,a是![]() 的立方根,方程
的立方根,方程![]() 是关于x,y的二元一次方程,d为不等式组
是关于x,y的二元一次方程,d为不等式组![]() 的最大整数解.
的最大整数解.
![]() 求点A、B、C的坐标;
求点A、B、C的坐标;
![]() 如图1,若D为y轴负半轴上的一个动点,当
如图1,若D为y轴负半轴上的一个动点,当![]() 时,
时,![]() 与
与![]() 的平分线交于M点,求
的平分线交于M点,求![]() 的度数;
的度数;
![]() 如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使![]() ?若存在,请求出D的纵坐标
?若存在,请求出D的纵坐标![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两仓库分别有水泥
两仓库分别有水泥![]() 吨和
吨和![]() 吨,
吨,![]() 、
、![]() 两工地分别需要水泥
两工地分别需要水泥![]() 吨和
吨和![]() 吨.已知从
吨.已知从![]() 、
、![]() 仓库到
仓库到![]() 、
、![]() 工地的运价如下表:
工地的运价如下表:
到 | 到 | |
| 每吨 | 每吨 |
| 每吨 | 每吨 |
1)若从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨,则用含
吨,则用含![]() 的代数式表示从
的代数式表示从![]() 仓库运到
仓库运到![]() 工地的水泥为_____吨,从
工地的水泥为_____吨,从![]() 仓库将水泥运到
仓库将水泥运到![]() 工地的运输费用为______元;
工地的运输费用为______元;
(2)求把全部水泥从![]() 、
、![]() 两仓库运到
两仓库运到![]() 、
、![]() 两工地的总运输费(用含
两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨时,那么总运输费为多少元?
吨时,那么总运输费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,AD=4,将△ABD沿着BD折叠,使点A与点E重合.
(1)如图,对角线AC、BD相交于点O,连接OE,则线段OE的长= ;
(2)如图,过点E作EF∥CD交线段BD于点F,连接AF,求证:四边形ABEF是菱形;
(3)如图,在(2)条件下,线段AE、BD相交于M,连接CE,求线段CE的长.
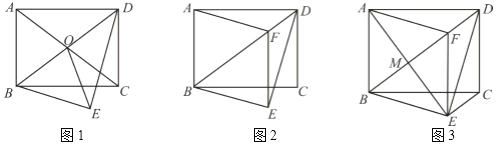
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、p满足![]() .
.
(1)求直线AP的解析式;
(2)如图1,点P关于y轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;
(3)如图2,点B(﹣2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②![]() 的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
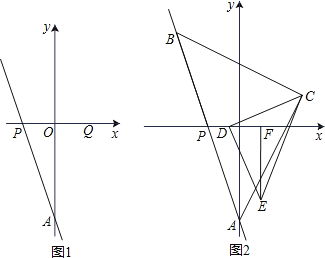
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在⊙O上,联结CO并延长交弦AB于点D, ![]() ,联结AC、OB,若CD=40,AC=20
,联结AC、OB,若CD=40,AC=20![]() .
.
(1)求弦AB的长;
(2)求sin∠ABO的值.
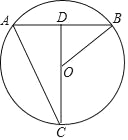
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com