
【题目】![]() 、
、![]() 两仓库分别有水泥
两仓库分别有水泥![]() 吨和
吨和![]() 吨,
吨,![]() 、
、![]() 两工地分别需要水泥
两工地分别需要水泥![]() 吨和
吨和![]() 吨.已知从
吨.已知从![]() 、
、![]() 仓库到
仓库到![]() 、
、![]() 工地的运价如下表:
工地的运价如下表:
到 | 到 | |
| 每吨 | 每吨 |
| 每吨 | 每吨 |
1)若从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨,则用含
吨,则用含![]() 的代数式表示从
的代数式表示从![]() 仓库运到
仓库运到![]() 工地的水泥为_____吨,从
工地的水泥为_____吨,从![]() 仓库将水泥运到
仓库将水泥运到![]() 工地的运输费用为______元;
工地的运输费用为______元;
(2)求把全部水泥从![]() 、
、![]() 两仓库运到
两仓库运到![]() 、
、![]() 两工地的总运输费(用含
两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨时,那么总运输费为多少元?
吨时,那么总运输费为多少元?
【答案】(1)(20-x),(9x+135);(2)(2x+525);(3)545元.
【解析】
(1)![]() 仓库原有的20吨减去运到
仓库原有的20吨减去运到![]() 工地的水泥,就是运到
工地的水泥,就是运到![]() 工地的水泥;首先求出
工地的水泥;首先求出![]() 仓库运到
仓库运到![]() 仓库的吨数,也就是
仓库的吨数,也就是![]() 工地需要的水泥减去从
工地需要的水泥减去从![]() 仓库运到
仓库运到![]() 工地的水泥,然后用
工地的水泥,然后用![]() 仓库运到
仓库运到![]() 仓库的吨数再乘每吨的运费即可;
仓库的吨数再乘每吨的运费即可;
(2)用![]() 表示出
表示出![]() 、
、![]() 两个仓库分别向
两个仓库分别向![]() 、
、![]() 运送的吨数,再乘每吨的运费,然后合并起来即可;
运送的吨数,再乘每吨的运费,然后合并起来即可;
(3)把![]() 代入(2)中的代数式,求得问题的解.
代入(2)中的代数式,求得问题的解.
解:(1)根据题意列表如下:
到 | 到 | |
| x | 20-x |
| 15-x | 35-(20-x)=15+x |
从A地运到D地的水泥为:(20-x),
从B地将水泥运到D地的运输费用为:9[35-(20-x)]=9x+135;
故答案为:(20-x),(9x+135);
(2)总运输费:15x+12(20-x)+10(15-x)+9[35-(20-x)]=(2x+525)元;
(3)当![]() 时,2x+525=2×10+525=545(元)
时,2x+525=2×10+525=545(元)
答:总运费为545元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交点为O,正方形OEFG的边长与正方形ABCD的边长相等,若将正方形OEFG绕点O旋转,试说明旋转到如图的位置时,两正方形重叠部分的面积与正方形面积之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人用![]() 元购买了
元购买了![]() 套儿童服装,准备以一定价格出售,如果以每套儿童服装
套儿童服装,准备以一定价格出售,如果以每套儿童服装![]() 元的价格为标准,超出的记作正数,不足的记作负数,记录如下:
元的价格为标准,超出的记作正数,不足的记作负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .(单位:元)
.(单位:元)
(1)最高售价比最低高出多少?
(2)当他卖完这![]() 套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
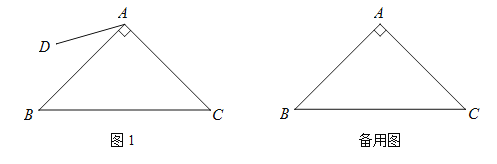
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 经过某种变换后得到点
经过某种变换后得到点![]() ,我们把点
,我们把点![]() 叫做点
叫做点![]() 的终结点.已知点
的终结点.已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() 、…
、…![]() 、…,若点
、…,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:![]() ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.
其中,正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com