
【题目】如图,直线l过正方形ABCD的顶点B,点A、C至直线l的距离分别为2和3,则此正方形的面积为( )
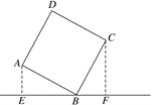
A. 5 B. 6 C. 9 D. 13
【答案】D
【解析】
由ABCD为正方形得到AB=BC,∠ABC为直角,再由AE与CF都垂直于EF,利用同角的余角相等得到一对角相等,再由一对直角相等,利用AAS得出△ABE与△BCF全等,由全等三角形对应边相等得到AE=BF,EB=CF,在直角三角形ABE中,利用勾股定理求出AB的长,即可确定出正方形的面积.
解:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠BAE+∠ABE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
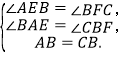
∴△ABE≌△BCF(AAS),
∴AE=BF=2,CF=EB=3,
根据勾股定理得:AB=![]() =
=![]() ,
,
则正方形ABCD面积为13.
故选D.


科目:初中数学 来源: 题型:
【题目】新合作超市最近进了一批玩具,进价每个15元,今天共卖山20个,实际卖出的价格以每个18元为标准,超过的记为正,不足的记为负,记录如下:
实际每个售出价格与标准的差值(单位:元) | +3 | -1 | +2 | +1 |
个数 | 5 | 4 | 6 | 5 |
(1)这个超市今天卖出玩具的平均价格是多少?
(2)这个超市今天卖出的玩具赚了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).
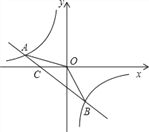
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F是对角线BD上的两点,且BE=DF.

(1)求证:四边形AECF是平行四边形.
(2)如果四边形ABCD是菱形,求证:四边形AECF也是菱形.
(3)如果四边形ABCD是矩形,请判断四边形AECF的形状,不必写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,a是
,a是![]() 的立方根,方程
的立方根,方程![]() 是关于x,y的二元一次方程,d为不等式组
是关于x,y的二元一次方程,d为不等式组![]() 的最大整数解.
的最大整数解.
![]() 求点A、B、C的坐标;
求点A、B、C的坐标;
![]() 如图1,若D为y轴负半轴上的一个动点,当
如图1,若D为y轴负半轴上的一个动点,当![]() 时,
时,![]() 与
与![]() 的平分线交于M点,求
的平分线交于M点,求![]() 的度数;
的度数;
![]() 如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使![]() ?若存在,请求出D的纵坐标
?若存在,请求出D的纵坐标![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两仓库分别有水泥
两仓库分别有水泥![]() 吨和
吨和![]() 吨,
吨,![]() 、
、![]() 两工地分别需要水泥
两工地分别需要水泥![]() 吨和
吨和![]() 吨.已知从
吨.已知从![]() 、
、![]() 仓库到
仓库到![]() 、
、![]() 工地的运价如下表:
工地的运价如下表:
到 | 到 | |
| 每吨 | 每吨 |
| 每吨 | 每吨 |
1)若从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨,则用含
吨,则用含![]() 的代数式表示从
的代数式表示从![]() 仓库运到
仓库运到![]() 工地的水泥为_____吨,从
工地的水泥为_____吨,从![]() 仓库将水泥运到
仓库将水泥运到![]() 工地的运输费用为______元;
工地的运输费用为______元;
(2)求把全部水泥从![]() 、
、![]() 两仓库运到
两仓库运到![]() 、
、![]() 两工地的总运输费(用含
两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨时,那么总运输费为多少元?
吨时,那么总运输费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com