
【题目】如图,正方形ABCD的对角线交点为O,正方形OEFG的边长与正方形ABCD的边长相等,若将正方形OEFG绕点O旋转,试说明旋转到如图的位置时,两正方形重叠部分的面积与正方形面积之间的关系.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】⊙O的半径为5cm,AB,CD是⊙O的两条弦,AB‖CD,AB=8,CD=6,AB和CD之间的距离是___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
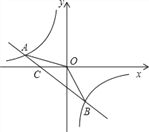
【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F是对角线BD上的两点,且BE=DF.

(1)求证:四边形AECF是平行四边形.
(2)如果四边形ABCD是菱形,求证:四边形AECF也是菱形.
(3)如果四边形ABCD是矩形,请判断四边形AECF的形状,不必写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,a是
,a是![]() 的立方根,方程
的立方根,方程![]() 是关于x,y的二元一次方程,d为不等式组
是关于x,y的二元一次方程,d为不等式组![]() 的最大整数解.
的最大整数解.
![]() 求点A、B、C的坐标;
求点A、B、C的坐标;
![]() 如图1,若D为y轴负半轴上的一个动点,当
如图1,若D为y轴负半轴上的一个动点,当![]() 时,
时,![]() 与
与![]() 的平分线交于M点,求
的平分线交于M点,求![]() 的度数;
的度数;
![]() 如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使![]() ?若存在,请求出D的纵坐标
?若存在,请求出D的纵坐标![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上,点![]() 的初始位置表示的数为
的初始位置表示的数为![]() ,现点
,现点![]() 做如下移动,第1次点
做如下移动,第1次点![]() 向左移动3个单位长度至点
向左移动3个单位长度至点![]() ,第2次从点
,第2次从点![]() 向右移动6个单位长度至点
向右移动6个单位长度至点![]() ,第
,第![]() 次从点
次从点![]() 向左移动
向左移动![]() 个单位长度至点
个单位长度至点![]() ,…,按照这种移动方式进行下云,如果点
,…,按照这种移动方式进行下云,如果点![]() 与原点的距离不小于
与原点的距离不小于![]() ,那么
,那么![]() 的最小值是___.
的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两仓库分别有水泥
两仓库分别有水泥![]() 吨和
吨和![]() 吨,
吨,![]() 、
、![]() 两工地分别需要水泥
两工地分别需要水泥![]() 吨和
吨和![]() 吨.已知从
吨.已知从![]() 、
、![]() 仓库到
仓库到![]() 、
、![]() 工地的运价如下表:
工地的运价如下表:
到 | 到 | |
| 每吨 | 每吨 |
| 每吨 | 每吨 |
1)若从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨,则用含
吨,则用含![]() 的代数式表示从
的代数式表示从![]() 仓库运到
仓库运到![]() 工地的水泥为_____吨,从
工地的水泥为_____吨,从![]() 仓库将水泥运到
仓库将水泥运到![]() 工地的运输费用为______元;
工地的运输费用为______元;
(2)求把全部水泥从![]() 、
、![]() 两仓库运到
两仓库运到![]() 、
、![]() 两工地的总运输费(用含
两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨时,那么总运输费为多少元?
吨时,那么总运输费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,健民体育活动中心从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据健民体育活动中心消费者的需求量,活动中心决定用不超过2550元钱购进甲、乙两种羽毛球共50筒,那么最多可以购进多少筒甲种羽毛球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com