
【题目】如图,矩形![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)求线段![]() 的长.
的长.
【答案】(1)见解析(2)![]()
【解析】
(1)根据矩形的性质得到CD=AB=8,AD=BC=4,CD∥AB,∠D=∠B=90°,求得CF=AE=83=5,根据勾股定理得到AF=CE=![]() =5,于是得到结论;
=5,于是得到结论;
(2)过F作FH⊥AB于H,得到四边形AHFD是矩形,根据矩形的性质得到AH=DF=3,FH=AD=4,根据勾股定理即可得到结论.
(1)证明:∵在矩形ABCD中,AB=8,BC=4,
∴CD=AB=8,AD=BC=4,CD∥AB,∠D=∠B=90°,
∵BE=DF=3,
∴CF=AE=83=5,
∴AF=CE=![]() =5,
=5,
∴AF=CF=CE=AE=5,
∴四边形AECF是菱形;
(2)解:过F作FH⊥AB于H,
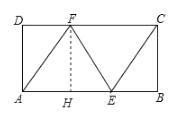
则四边形AHFD是矩形,
∴AH=DF=3,FH=AD=4,
∴EH=5-3=2,
∴EF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:

(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]()

如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,![]()
![]() ,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21,
,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21,![]() ,求图4中所有圆圈中各数的绝对值之和.
,求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
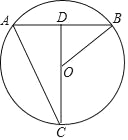
【题目】如图,点C在⊙O上,联结CO并延长交弦AB于点D, ![]() ,联结AC、OB,若CD=40,AC=20
,联结AC、OB,若CD=40,AC=20![]() .
.
(1)求弦AB的长;
(2)求sin∠ABO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美化城市,改善人们的居住环境已成为城市建设的一项重要内容。某市城区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加(如图所示).
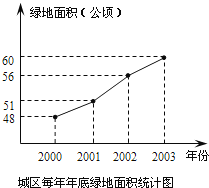
(1)根据图中所提供的信息,回答下列问题:2003年底绿地面积为____公顷,比2002年底增加了_____公顷;在2000年、2001年、2002年这三年中,绿地面积增加最多是_______年.
(2)为满足城市发展的需要,计划到2005年底使城区绿地总面积达到72.6公顷,试求2003年到2005年绿地面积的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
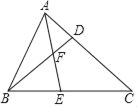
【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若![]() ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=![]() ∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
A.(1)(2)B.(1)(2)(4)C.(2)(3)(4)D.(1)(3)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com