
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,
内一点,![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() .
.
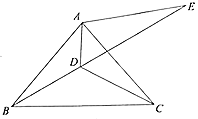
(1)求![]() 的度数;
的度数;
(2)求证:![]() 平分
平分![]() ;
;
(3)请判断![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)![]() ;(2)见解析;(3)结论:
;(2)见解析;(3)结论:![]() ,见解析.
,见解析.
【解析】
(1)由等腰三角形的性质可得∠ABC=∠ACB,根据角的和差关系可得∠DBC=∠DCB,可得BD=CD,利用SAS可证明△ADB≌△ADC,可得∠BAD=∠CAD,即可求出∠BAD的度数;
(2)利用三角形外角性质可得∠ADE=60°,根据三角形内角和定理可得∠ABC=∠ACB=50°,即可得出![]() =30°,利用外角性质可得∠CDE=60°,即可证明∠ADE=∠CDE,可得
=30°,利用外角性质可得∠CDE=60°,即可证明∠ADE=∠CDE,可得![]() 平分
平分![]() ;
;
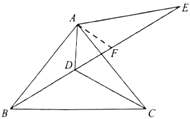
(3)在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,根据等腰三角形的性质可得∠ABE=∠E,由DF=DA,∠ADE=60°可证明△ADF是等边三角形,可得
,根据等腰三角形的性质可得∠ABE=∠E,由DF=DA,∠ADE=60°可证明△ADF是等边三角形,可得![]() ,利用AAS可证明
,利用AAS可证明![]() ,可得BD=EF,即可证明
,可得BD=EF,即可证明![]() .
.
(1)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() .
.
(3)结论:![]() ,
,
在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
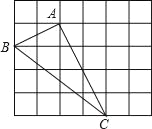
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为_____;
(3)△ACD为 三角形,四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
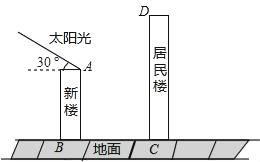
【题目】某住宅小区有一栋面朝正南的居民楼(如图),该居民楼的一楼高为6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.已知冬季正午的阳光与水平线的夹角为30°时.
(1)新楼的建造对超市以上的居民住房冬季正午的采光是否有影响,为什么?
(2)若要使超市冬季正午的采光不受影响,新楼应建在相距居民楼至少多少米的地方,为什么?(结果保留整数,参考数据:sin30°≈0.5,cos30°≈0.87,tan30°≈0.58)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
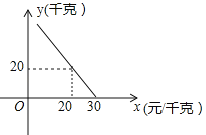
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com