
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

【答案】(1)详见解析;(2)60°.
【解析】
试题分析:(1)由作图过程可知,AB=AF,AE平分∠BAD,即可得∠BAE=∠EAF.再由四边形ABCD为平行四边形,可得BC∥AD,根据平行线的性质可得∠AEB=∠EAF,所以∠BAE=∠AEB,根据等腰三角形的性质可得AB=BE,即可得BE=AF,所以四边形ABEF为平行四边形,根据一组邻边相等的平行四边形是菱形即可判定四边形ABEF为菱形;(2)连接BF,已知四边形ABEF为菱形,根据菱形的性质可得BF与AE互相垂直平分,∠BAE=∠FAE,OA=![]() AE=
AE=![]() .再由菱形ABEF的周长为16,可得AF=4.所以cos∠OAF=
.再由菱形ABEF的周长为16,可得AF=4.所以cos∠OAF=![]() =
=![]() .即可得∠OAF=30°,所以∠BAF=60°.再由平行线的性质即可得∠C=∠BAD=60°.
.即可得∠OAF=30°,所以∠BAF=60°.再由平行线的性质即可得∠C=∠BAD=60°.
试题解析:
(1)由作图过程可知,AB=AF,AE平分∠BAD.∴∠BAE=∠EAF.
∵四边形ABCD为平行四边形,∴BC∥AD.∴∠AEB=∠EAF.
∴∠BAE=∠AEB,∴AB=BE.∴BE=AF.∴四边形ABEF为平行四边形.
∴四边形ABEF为菱形.
(2)连接BF,
![]()
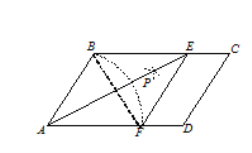
∵四边形ABEF为菱形,∴BF与AE互相垂直平分,∠BAE=∠FAE.
∴OA=![]() AE=
AE=![]() .∵菱形ABEF的周长为16,∴AF=4.
.∵菱形ABEF的周长为16,∴AF=4.
∴cos∠OAF=![]() =
=![]() .∴∠OAF=30°,∴∠BAF=60°.
.∴∠OAF=30°,∴∠BAF=60°.
∵四边形ABCD为平行四边形,∴∠C=∠BAD=60°.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
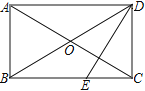
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF= ![]() ,BD=2,则菱形ABCD的面积为( )
,BD=2,则菱形ABCD的面积为( ) 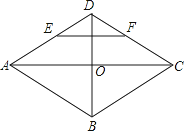
A.2 ![]()
B.![]()
C.6 ![]()
D.8 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.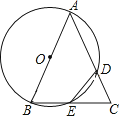
(1)求证:AB=AC;
(2)若AB=4,BC=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家(记为A)、他上学的学校(记为B)、书店(记为C)依次坐落在一条东西走向的大街上,小明家位于学校西边250米处,书店位于学校东边100米处,小明中午放学后,到书店买本辅导书,然后回家吃中午饭,下午直接去学校上课.
(1)试用数轴表示出小明家(A)、学校(B)、书店(C)的位置;
(2)计算出小明家与书店的距离;
(3)小明从中午放学离校到下午上学到校一共走了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 . 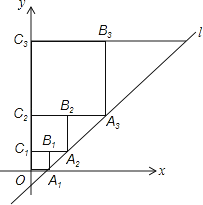
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 ![]() 与
与 ![]() 轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与
轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与 ![]() 轴交于点C(0,-3),顶点为D。
轴交于点C(0,-3),顶点为D。
(1)求抛物线的解析式及顶点D的坐标。
(2)联结AC,BC,求∠ACB的正切值。
(3)点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由。
(4)M是抛物线上一点,点N在 ![]() 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。
轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com