
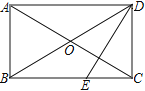
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
【答案】(1)证明见解析(2)18°
【解析】
(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;
(2)求出∠ADB的度数,根据三角形内角和定理求出∠AOB,从而可得到∠CDO,最后,依据∠BDE=90°-∠DOC求解即可.
(1)∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)∵∠ADC=90°,∠ADB:∠CDB=2:3,
∴∠ADB=36°,
∵四边形ABCD是矩形,
∴OA=OD,
∴∠OAD=∠ADB=36°,
∴∠DOC=72°,
∵DE⊥AC,
∴∠BDE=90°-∠DOC=18°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有一个种植总面积为540 m2的长方形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:

(1)若设草莓共种植了x垄,请说明共有几种种植方案,分别是哪几种;
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
请结合图表完成下列各题:
(1)①求表中a的值;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率. 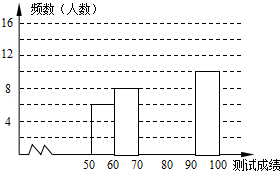
查看答案和解析>>
科目:初中数学 来源: 题型:
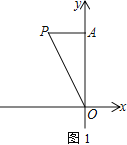
【题目】如图,平面直角坐标系中,已知点A(0,5),点P(m,5)在第二象限,连接AP、OP
(1) 如图1,若OP=6,求m的值
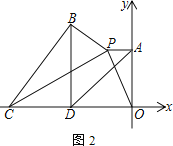
(2) 如图2,点C在x轴负半轴上,以CP为斜边作直角三角形BCP,∠CBP=90°,且∠BPC=∠APO.取OC的中点D,连接AD、BD,求证:AD=BD
(3) 如图3,将△AOP沿直线OP翻折得到△EOP(点A的对应点为点E).若点E到x轴的距离不大于3,直接写出m的取值范围(无需解答过程)
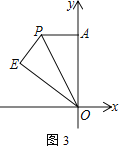
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图. 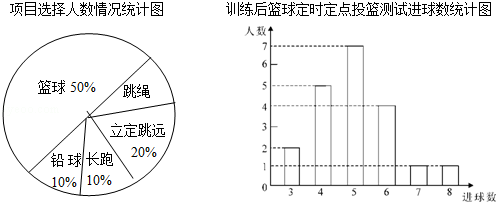
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为度,该班共有学生人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=-2x与直线l2:y=kx+b在同一平面直角坐标系内交于点P .
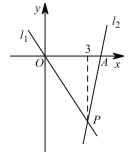
(1)直接写出不等式-2x>kx+b 的解集 ;
(2)设直线l2 与x 轴交于点A ,△OAP的面积为12 ,求l2的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com